Test-time-computing
날짜: 2025년 2월 27일
개요
- 대형 언어 모델(LLM)의 발전
- 컴퓨팅 자원 확장이 큰 영향 → 큰 모델 훈련 = 지나치게 비쌈
- 보조적인 접근법인 테스트 시간 컴퓨팅 확장에 대한 관심 증가
- 큰 훈련 예산을 사용하는 대신, 모델이 어려운 문제를 풀 때 더 긴 시간을 들여 생각할 수 있게 하는 동적인 추론 전략을 사용
- 그 중 하나가 OpenAI의 o1 모델로, 테스트 시간 컴퓨팅을 늘림으로써 어려운 수학 문제에서 일관되게 성능이 향상

- DeepMind의 최근 연구: 테스트 시간 컴퓨팅을 최적으로 확장할 수 있는 전략 제시
- 반복적인 자기 정제나 보상 모델을 사용해 탐색하는 방법
- 더 작은 모델이 더 크고 자원이 많이 드는 모델을 능가, 비슷한 성능
- 특히 메모리가 제한적, 더 큰 모델을 실행할 수 있는 하드웨어가 부족할 때 유리
- closed model 로만 사용이 많이 되었고, 구현 세부 사항, 코드 공개 없었음
- 본 글은 다음 내용 다룸
- 컴퓨팅 최적화 확장: DeepMind의 방법을 구현, 개방형 모델의 수학적 능력을 테스트 시간에 향상시키는 방법.
- 다양성 검증 트리 탐색(DVTS): 검증자 기반 트리 탐색 기법을 개선한 비공개 확장, 더 큰 테스트 시간 컴퓨팅 예산에서 성능과 다양성을 높이는 간단하지만 효과적인 방법.
- 검색과 학습(Search and Learn): LLM을 위한 검색 전략을 구현하는 경량 툴킷, vLLM을 사용하여 속도에 최적화된 도구.
- 예시) 1B와 3B Llama Instruct 모델이 8B와 70B 모델보다 MATH-500 벤치마크에서 더 높은 성능
- 반복적인 자기 정제나 보상 모델을 사용해 탐색하는 방법

Strategies for test-time compute scaling
- 테스트 시간 컴퓨팅 확장에는 두 가지 주요 전략
- 자기 정제(Self-Refinement)
- 모델이 반복적으로 자신이 생성한 출력이나 "생각"을 정제, 후속 반복에서 오류를 식별하고 수정하는 방식
- 모델이 자체 정제를 위한 메커니즘을 내장하고 있어야 하므로 적용 가능성이 제한적일 수 있음
- 검증자를 통한 검색(Search Against a Verifier)
- 여러 후보 답안을 생성, 검증자를 사용해 최선의 답을 선택하는 방식
- 검증자는 하드코딩된 휴리스틱부터 학습된 보상 모델까지 다양
- 검색 전략은 문제의 난이도에 따라 적응할 수 있는 장점, 성능은 검증자의 품질에 제한
- 본 글:
- 아래 세 가지 전략 다룸 (검색 기반 방법, 학습된 검증자에 초점)
- Best-of-N
- 문제당 여러 개의 응답을 생성
- 각 후보 답변에 점수를 부여 → 가장 높은 점수를 받은 답을 선택하는 방법
- 빈도보다 답의 품질을 강조
- 빔 탐색(Beam Search)
- 해결책 공간을 체계적으로 탐색하는 방법
- 종종 과정 보상 모델(PRM) 과 결합되어 문제 해결 중간 단계의 샘플링 및 평가를 최적화
- 전통적인 보상 모델: 최종 답에 대한 하나의 점수를 제공
- PRM: 추론 과정의 각 단계에 대해 순차적으로 점수를 제공
- 다양성 검증자 트리 탐색(DVTS)
- 빔 탐색을 확장한 방법
- 초기 빔을 독립적인 서브트리로 나눈 후, PRM을 사용해 그들을 탐색
- 여러 후보 답안을 생성, 검증자를 사용해 최선의 답을 선택하는 방식

Experimental setup
- 파이프라인
- 문제 입력: 수학 문제를 LLM에 입력하면, LLM은 중간 단계의 해결책(예: 유도 과정의 중간 단계)을 생성
- 단계별 평가: 각 단계는 과정 보상 모델(PRM) 에 의해 평가, 각 단계가 최종적으로 올바른 답에 도달할 확률을 추정, 이 단계와 PRM 점수는 주어진 검색 전략에 의해 사용되어, 어떤 중간 해결책을 더 탐색할지 결정
- 다음 단계 생성: 검색 전략이 종료되면, PRM을 사용해 최종 후보 해결책들을 순위별로 평가하고 최종 답을 도출
- 모델: 테스트 시간 컴퓨팅 확장을 위한 주요 모델로 meta-llama/Llama-3.2-1B-Instruct 를 사용
- 과정 보상 모델
- 검색 전략을 유도하기 위해 RLHFlow/Llama3.1-8B-PRM-Deepseek-Data 라는 8B 보상 모델을 사용
- 과정 감독 방식으로 훈련
- 과정 감독: 모델이 최종 결과만 아니라 각 추론 단계에 대해 피드백을 받는 훈련 방식
- 정책 모델과 동일한 모델 계열
- 데이터셋:
- MATH-500 벤치마크의 하위 집합을 사용해 평가
- OpenAI의 연구에서 공개
- 수학 문제 7개 분야
- 각 검색 전략을 1부터 256까지의 다양한 컴퓨팅 예산 범위에서 테스트
- 5개의 랜덤 시드를 사용하여 실행 간 변동성을 추정
베이스라인: 다수결 (Majority voting)
- 다수결 혹은 자기 일관성 디코딩(self-consistency decoding): 주어진 수학 문제에 대해 여러 개의 후보 해결책을 생성 → 가장 빈도가 높은 답을 선택하는 방식
- 최대 n=256 개의 후보를 샘플링하고, temperature T=0.8, 각 문제마다 최대 2048개의 토큰을 생성
- 결과
- Greedy decoding (일반 생성, baseline) 방식보다는 상당한 개선
- N=64 이후에는 성능 향상 멈추는 경향, 다수결 투표 방식이 복잡한 추론을 필요로 하거나 세밀한 오류 처리에서 어려움
- 다수결 투표의 정확도가 N=1과 2일 때 0-shot CoT(Chain of Thought) 방식보다 낮은 이유는, T=0.8로 샘플링을 하기 때문에 올바른 답을 덜 생산할 가능성이 높기 때문
- 다수결 투표의 한계를 극복 방안: 보상 모델(reward model)을 도입해 성능을 향상
Beyond majority: Best-of-N
- 다수결의 확장 방식, 보상 모델을 사용하여 가장 그럴듯한 답을 선택하는 방식
- 두 가지 주요 변형
- Vanilla Best-of-N: 독립적인 응답을 여러 개 생성하고, 보상 모델(RM)에서 가장 높은 점수를 받은 응답을 최종 답으로 선택
- Weighted Best-of-N: 동일한 응답들에 대해 점수를 합산하여 총 보상이 가장 높은 답을 선택
- 보상 모델 점수 계산
- Min: 각 단계별 점수 중에서 가장 낮은 점수를 최종적으로 답안의 점수로 간주
- Prod: 각 단계에서 얻은 점수들을 곱한 값을 사용
- 여러 단계에서 점수가 높을수록 최종 점수도 커지지만, 어느 하나라도 점수가 0에 가까워지면 전체 점수가 매우 낮아지기 때문에 각 단계에서의 고른 성능이 중요
- Last: 마지막 단계의 점수를 사용
- 문제 해결의 마지막 단계에서 가장 중요한 정보를 고려하고, 전체 과정에서의 누적된 정보를 평가하는 방식
- 실험 결과: Last 방식이 가장 우수한 성능
- cf) Vanilla Best-of-N은 max 방식으로 동작

- 결과
- Weighted Best-of-N은 Vanilla Best-of-N보다 consistently 더 우수한 성능
- 더 많은 generation (=생성 sample) 할 때 차이가 더 커짐
- 여전히 생성 수가 어느정도 도달하면 성능이 정체되는 경향
- 해결 방안: 검색 과정(step-by-step search process) 감독하는 방법

Beam search with process reward models
- Beam Search와 보상 모델(PRM)을 결합한 방식
- 주어진 문제를 해결하는 중간 단계를 최적화하고 평가하는 데 유용
- 점진적으로 여러 후보 솔루션을 생성, 각 단계에서 얻은 보상 모델 점수를 바탕으로 최선의 경로를 선택
- Beam Search의 동작 방식
- 여러 후보 솔루션을 생성:
- 정해진 수의 경로(beam) 유지, 후보 생성
- 독립적인 답안을 여러 개 샘플링(=다양성 고려)
- 각 후보는 보상 모델(PRM)을 통해 평가되며, 평가 점수가 높은 상위 후보만 선택
- 보상 모델을 통한 평가
- last 방식으로 점수 계산, 상위 N개 경로 선택
- 다음 단계로 확장: 선택된 경로를 확장하여 다음 단계의 솔루션을 생성, (이 과정 반복)
- 최종 답안 선택: EOS(End Of Sequence) 토큰에 도달하거나, 최대 깊이에 도달하면 최종 답안을 선택
- 여러 후보 솔루션을 생성:
- 결과
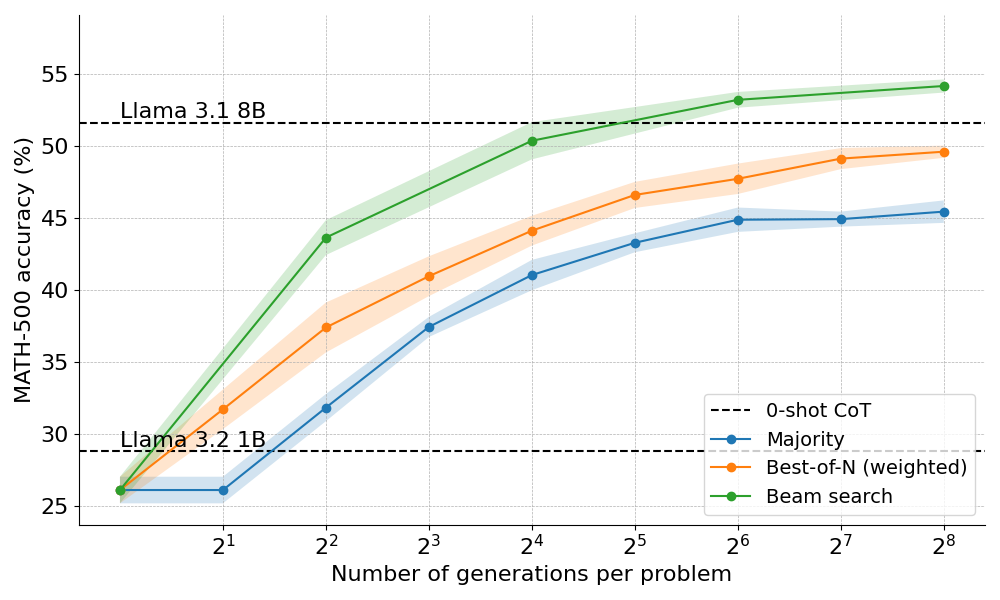
- Beam Search는 다양한 컴퓨팅 예산에서 Best-of-N보다 뛰어난 성과
- Llama 3.1 8B 모델의 성능을 넘는 결과를 1B 모델만으로도 달성
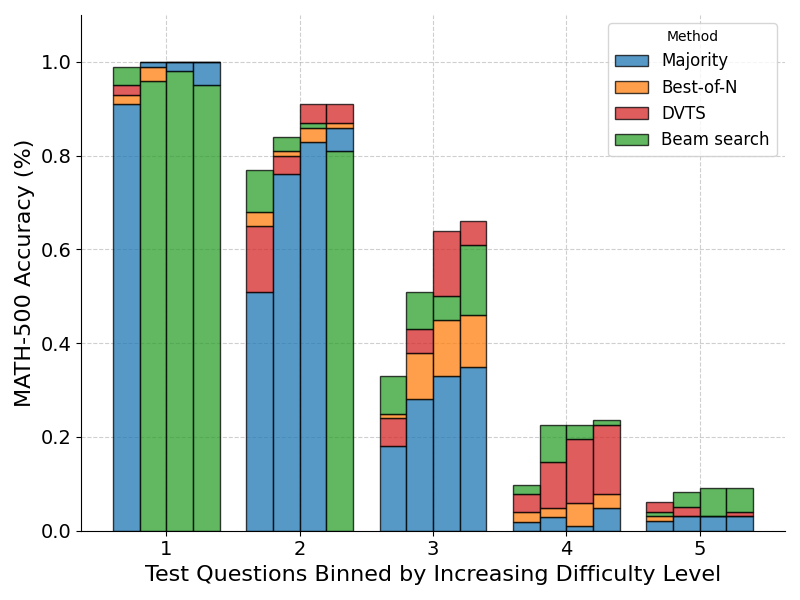
- Beam Search는 중간 및 어려운 문제에서는 Best-of-N 또는 Majority Voting이 더 나은 성능
- 간단한 문제에서는 Best-of-N이나 Majority Voting이 더 나을 수 있음
- 다양성 이슈: 하나의 단계에서 높은 보상 점수가 부여되면, 전체 트리가 그 경로로 집중, 다양성 부족 문제 발생 가능

DVTS: boosting performance with diversity
- DVTS (Diverse Verifier Tree Search)
- Beam Search의 성능을 보완, 다양성을 극대화하여 특히 큰 테스트 시간 예산에서 좋은 성과
- DVTS의 동작 방식
- 초기 설정: beam width와 최대 깊이에 따라, 초기 beam을 여러 개의 독립적인 서브트리로 확장
- 각 서브트리에서 최고 점수 선택: 각 서브트리에서 보상 모델 점수가 가장 높은 단계를 선택
- 새로운 단계 생성: 선택된 단계에서 새로운 단계를 생성하고, 다시 보상 모델 점수가 가장 높은 단계를 선택
- 반복, 최종 선택: EOS 토큰 도달, 최대 깊이 도달
- 결과
- Beam Search는 작은 예산에서 더 효과적이며, 쉬운 문제에서 뛰어난 성능을 보입니다.
- DVTS는 쉬운/중간 난이도 문제에서 큰 예산을 사용할 때 더 나은 성과를 보이고, 다양한 후보를 생성하여 문제 해결에 유리한 방식입니다.

'Development > Python' 카테고리의 다른 글
| [코딩테스트#1] 기초 자료 구조: 배열, 문자열, 스택, 큐 (1) | 2024.06.23 |
|---|---|
| [파이썬 부트캠프 #2] 데이터 형식의 이해 및 문자열 조작 방법 (1) | 2023.09.03 |
| [파이썬 부트캠프 #1] 파이썬 변수를 사용한 데이터 관리 (0) | 2023.07.28 |


