

목차
챕터5. 자료 구조
- 자료구조 data structure: 효율적으로 데이터를 관리, 수정, 삭제, 탐색, 저장할 수 있는 데이터 집합
- 본 책 C++ 기반으로 자료 구조 설명 예정
5.1 복잡도
- 복잡도: 시간 복잡도, 공간 복잡도
5.1.1 시간 복잡도
- 시간 복잡도: 문제를 해결하는 데 걸리는 시간과 입력의 함수 관계
- 빅오 표기법:
- 입력 범위 n을 기준으로 해서 로직이 몇 번 반복되는지 나타내느 것
- 가장 영향을 많이 끼치는 항의 상수 인자를 빼고 나머지 항을 없앤 것
- $10n^2+n$ → $O(n^2)$
- 시간 복잡도의 존재 이유: 효율적인 코드로 개선하는 데 쓰이는 척도
5.1.2 공간 복잡도
- 공간 복잡도: 프로그램을 실행시켰을 때 필요로 하는 자원 공간의 양
- 정적 변수로 선언된 것 말고도 동적으로 재귀적인 함수로 인해 공간을 계속해서 필요로 할 경우도 포함
5.1.3 자료 구조에서의 시간 복잡도
- 시간 복잡도를 생각할 때, 평균, 최악의 시간 복잡도를 고려


5.2 선형 자료 구조
- 선형 자료 구조: 요소가 일렬로 나열되어 있는 자료 구조
5.2.1 연결 리스트
- 연결 리스트: 데이터를 감싼 노드를 포인트로 연결해서 공간적인 효율성을 극대화시킨 자료 구조
- 삽입, 삭제 시간 복잡도 O(1)
- 탐색 O(n)
- prev 포인터와 next 포인터로 앞과 뒤의 노드를 연결
- 종류
- 싱글 연결 리스트: next 포인터만 가짐
- 이중 연결 리스트: next 포인터와 prev 포인터를 가짐
- 원형 이중 연결 리스트: 이중 연결 리스트와 유사, 마지막 노드의 next 포인터가 헤드 노드를 가르킴

5.2.2 배열
- 배열:
- 같은 타입의 변수들로 이루어져 있고,
- 크기가 정해져 있음
- 인접한 메모리 위치에 있는 데이터를 모아놓은 집합
- 중복 허용, 순서 있음
- 정적 배열 기준
- 탐색 시간 복잡도 O(1) → 랜덤 접근 가능
- 삽입, 삭제 시간 복잡도 O(n)
- 랜덤 접근, 순차적 접근
- 랜덤 접근(=직접 접근): 동일한 시간에 배열과 같은 순차적인 데이터가 있을 때, 임의의 인덱스에 해당하는 데이터에 접근
- 순차적 접근: 데이터를 저장된 순서대로 검색
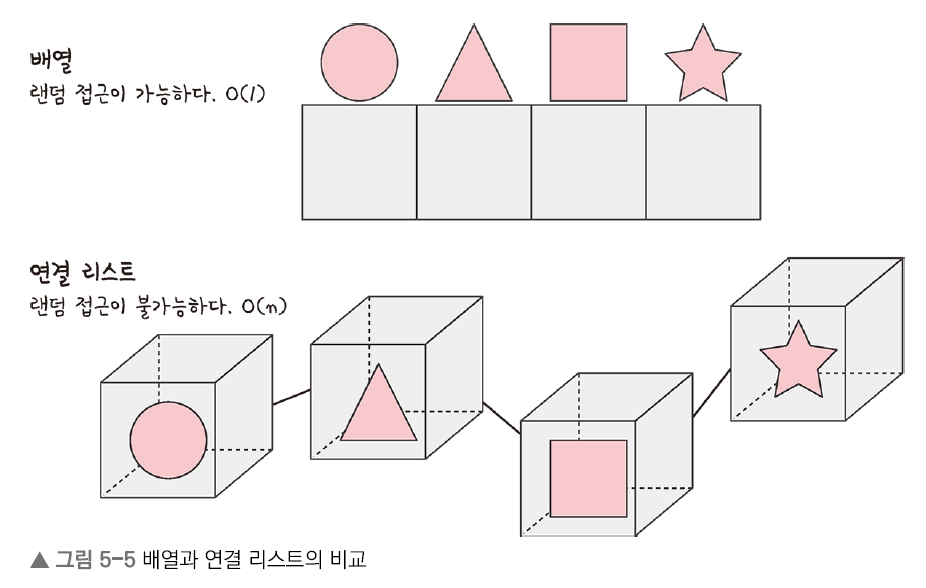
- 배열과 연결 리스트
- 배열:
- 상자를 순서대로 나열한 데이터 구조
- 몇 번째 상자인지만 알면 해당 상자의 요소 사용 가능
- 탐색이 빠름
- 연결 리스트:
- 상자를 선으로 연결한 형태의 데이터 구조
- 상자 안의 요소를 알기 위해서는 하나씩 상자 내부를 확인해봐야 함
- 데이터 추가 및 삭제 빠름
- 배열:
5.2.3 벡터
- 벡터:
- 동적으로 요소를 할당할 수 있는 동적 배열
- 컴파일 시적에 개수를 모른다면 벡터를 사용해야 함
- 중복 허용, 순서 존재, 랜덤 접근 가능
- 탐색, 맨 뒤 요소 삭제 시간 복잡도: O(1)
- 벡터의 크기가 증가되는 시간 복잡도: amortized 복잡도, 상수 시간 복잡도 O(1)과 유사한 시간 복잡도를 가지기 때문
- 맨 앞뒤 아닌 요소 삭제, 삽입 시각 복잡도: O(n)
- 동적으로 요소를 할당할 수 있는 동적 배열
5.2.4 스택
- 가장 마지막으로 들어간 데이터가 가장 첫 번째로 나오는 성질(LIFO, Last In First Out)을 가진 자료 구조
- 재귀적인 함수, 알고리즘에 사용
- 삽입, 삭제 시간복잡도: O(1)
- 탐색 시간 복잡도: O(n)
5.2.5 큐
- 먼저 집어넣은 데이터가 먼저 나오는 성질(FIFO, First In First Out)을 지닌 자료 구조
- 스택과 반대 개념
- 삽입, 삭제 시간복잡도: O(1)
- 탐색 시간복잡도: O(n)
- CPU 작업을 기다리는 프로세스, 스레드 행렬, 네트워크 접속 행렬, 너비 우선 탐색, 캐시 등에 사용
5.3 비선형 자료 구조
- 비선형 자료 구조: 일렬로 나열하지 않고 자료 순서나 관계가 복잡한 구조
- 트리, 그래프 등
5.3.1 그래프
- 정점과 간선으로 이루어진 자료 구조
- “어떠한 곳에서 어떠한 곳으로 무언가를 통해서 간다”
- “어떠한 곳”: 정점 vertex, “무언가” 간선 edge
- 정점의 outdegree: 정점으로 나가는 간선
- 정점의 indegree: 정점으로 들어오는 간선
- “어떠한 곳에서 어떠한 곳으로 무언가를 통해서 간다”
- 그래프: 정점과 간선으로 이루어진 집합
5.3.2 트리
- 그래프 중 하나, 그래프의 특징처럼 정점과 간선으로 이루어짐
- 트리 구조로 배열된 일종의 계층적 데이터 집합
- 트리의 구성: 루트 노드, 내부 노드, 리프 노드
- 트리의 특징
- 부모, 자식 계층 구조를 가짐
- V-1=E라는 특징 → 간선 수 = 노드 수 -1
- 임의의 두 노드 사이의 경오는 무조건 존재
- 트리의 높이와 레벨
- 깊이: 루트 노드부터 특정 노드까지 최단 거리
- 높이: 루트 노드부터 리프 노드까지 거리 중 최장 거리
- 레벨: 주어지는 문제 마다 조금씩 다름, 보통 깊이와 같은 의미
- 서브 트리: 트리 내의 하위 집합
- 이진 트리: 자식의 노드 수가 두 개 이하인 트리
- 이진 탐색 트리(BST):
- 노드의 오른쪽 하위 트리에는 “노드 값보다 큰 값”이 있는 노드만 포함
- 왼쪽 하위 트리에는 “노드 값보다 작은 값”이 들어 있는 트리
- → 검색에 용이
- 원하는 요소를 찾을 때, 시간 복잡도: O(logn), O(n)(최악의 경우)
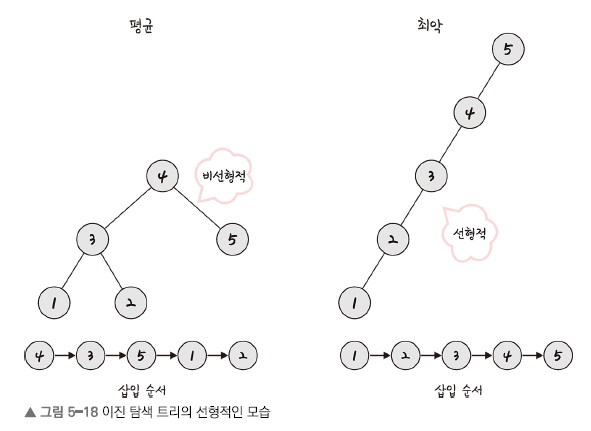
- AVL 트리:
- 최악의 경우인 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리
- 두 자식 서브트리의 높이는 항상 최대 1만큼 남
- 탐색, 삽입, 삭제 시간 복잡도: O(logn)
- 삽입, 삭제 시, 균형이 안 맞는 것을 맞추기 위해 트리 일부를 왼쪽, 오른쪽으로 회전시키며 균형을 잡음
- 최악의 경우인 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리

- 레드 블랙 트리
- 균형 이진 트리
- 탐색, 삽입, 삭제 시간 복잡도: O(logn)
- 각 노드는 빨간색 또는 검은색의 색상을 나타내는 추가 비트 저장
- 삽입 및 삭제 중에 트리가 균형을 유지하도록 하는데 사용
- 규칙: 모든 리프 노드와 루트 노드는 블랙
- 규칙: 어떤 노드가 레드이면 그 노드의 자식은 반드시 블랙

5.3.3 힙
- 완전 이진 트리 기반의 자료 구조
- 최대힙
- 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 큼(각 노드의 자식 노드도 동일)
- 최대힙의 삽입:
- 새로운 노드를 힙의 마지막 노드에 이어서 삽입
- 새로운 노드를 부모 노드들과의 크기를 비교하며 교환해서 힙의 성질을 만족시킴
- 최대힙의 삭제
- 최댓값은 루트 노드 → 루트 노드가 삭제
- 마지막 노드와 루트 노드를 스왑, 스왑 등의 과정을 거쳐 재구성

- 최소힙
- 루트 노드에 있는 키는 모든 자식에 있는 키 중에서 가장 작음(각 노드의 자식 노드도 동일)
5.3.4 우선순위 큐
- (=우선순위 대기열)
- 대기열에서 우선순위가 높은 요소가 우선순위가 낮은 요소보다 먼저 제공되는 자료 구조
- 힙을 기반으로 구현
5.3.5 맵
- 특정 순서에 따라 키와 매핑된 값의 조합으로 형성된 자료 구조
- “이승철”: 1, “박동영”:2 같은 방식으로 string:int 형태
- 레드 블랙 트리 자료 구조 기반
- 삽입하면 자동으로 정렬
- map 순회 시, 키에 해당하는 값을 first, 키에 매핑된 값을 second로 탐색 가능
5.3.6 셋
- 특정 순서에 따라 고유한 요소를 저장하는 컨테이너
- 중복되는 요소는 없고 희소한(unique) 값만 저장하는 자료 구조
5.3.7 해시 테이블
- 무한에 가까운 데이터들을 유한한 개수의 해시 값으로 매핑한 테이블
- 삽입, 삭제, 탐색 시간 복잡도: (평균적) O(1)
'Boaz > Computer Science' 카테고리의 다른 글
| [CS 전공지식 #16] 챕터4-6~7. 조인과 조인의 원리 (0) | 2025.02.24 |
|---|---|
| [CS 전공지식 #15] 챕터4-4~5. 데이터베이스의 종류와 인덱스 (0) | 2025.02.24 |
| [CS 전공지식 #14] 챕터4-3. 트랜잭션과 무결정 (0) | 2025.02.24 |
| [CS 전공지식 #13] 챕터4-2. ERD와 정규화 과정 (0) | 2025.02.24 |
| [CS 전공지식 #12] 챕터4-1. 데이터베이스의 기본 (0) | 2025.02.24 |



