[강화학습 #1] 챕터1. 밴디트 문제

 

 

BOAZ 학기 중 스터디로 강화학습 스터디도 진행 중인데,

정리한 내용을 차차 올려보려고 합니다.

 

졸업 주제로 강화학습을 접목할 예정이라 보고 있는데

책이 워낙 잘 쓰여져서 그런지 개념이 잡히고 있는 느낌..!

 

노션에 정리한 기록을 옮기는 거라.. 식이 다 잘 들어갈지 걱정이 되는군요...

강화학습 차근차근 공부하실 분들께 이 책 추천합니다 :)

 

 

 

목차

1.1 머신러닝 분류와 강화 학습

1.2 밴디트 문제

1.3 밴디트 알고리즘

1.4 밴디트 알고리즘 구현

1.5 비정상 문제

 

 

챕터 1. 밴디트 문제

1.1 머신러닝 분류와 강화 학습

• 머신러닝 분류: 지도 학습, 비지도 학습, 강화 학습
• 지도 학습 supervised learning
  • 입력 (문제)과 출력(정답)을 쌍으로 묶은 데이터
  • ‘정답 레이블’ 이 존재
  • 사람의 손으로 정답 레이블을 만드는 일 ‘레이블링’, ‘어너테이션 annotation’ 이 필요
• 비지도 학습 unsupervised learning
  • ‘정답 레이블’ 없이 오직 데이터만 존재
  • 데이터에 숨어 있는 구조나 패턴을 찾는 용도로 주로 사용
  • 군집화(클러스터링), 특성 추출, 차원 축소 등
• 강화 학습 reinforcement learning
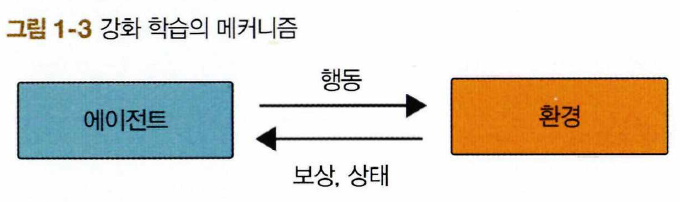
  • 에이전트와 환경이 서로 상호작용
    • 에이전트 agent: 행동 주체
    • 에이전트는 어떤 환경 environment에 있고, 환경의 상태 state를 관찰, 상태에 적합한 행동 action
    • 행동을 취하면 환경의 상태가 변화함
    • 에이전트는 환경으로부터 보상 reward을 받고, ‘새로운 상태’를 관찰
  • 강화 학습의 목표: 에이전트가 얻는 보상의 총합을 극대화하는 행동 패턴을 익히는 것

 

 

 

 

1.2 밴디트 문제

• 밴디트 문제
  • 밴디드 bandit = 슬롯머신
    • 정확하게는, 멀티-암드 밴디트 문제 multi-armed bandit problem
    • 손잡이 하나짜리 슬롯머신이 여러 대인 문제
  • 강화 학습 용어로 설명
    • 환경: 슬롯머신, 에이전트: 플레이어
    • 행동: 플레이어가 여러 슬롯머신 중 한대를 선택해 플레이
    • 보상: 플레이어가 슬롯머신에서 코인을 얻음
  • 목표: 코인을 최대한 많이 얻는 것
    • 승률이 ‘좋은 슬롯머신’ 선택 필요
• 좋은 슬롯머신이란?
  • 무작위한 정도를 확률을 이용해 정량적으로 설명
  • 확률 분포표 probability distribution table
  • 기댓값 expectation value
    • 플레이했을 때 얻을 수 있는 코인 개수의 평균
    • 더 높은 기댓값을 기준으로 슬롯머신을 선택
  • 밴디트 문제
    • 보상의 기댓값 → 가치 value
    • 행동의 결과로 얻는 보상의 기댓값 → 행동 가치 action value
• 수식으로 표현하기
  • 보상 Reward → $R$
  • 에이전트가 수행하는 행동 Aciont → $A$
    • 행동을 각각 a와 b → 변수 A는 {a,b} 중 하나 값을 취하게 됨
  • 기댓값 Expectation → $E$
    • 보상 R의 기댓값 E[R]
    • 행동 A를 선택했을 때의 보상 기댓값 E[R|A]
  • 행동 가치: 보상에 대한 기댓값 → Q 또는 q
    • 행동 A의 행동 가치 q(A)
    • $q(A)=E[R|A]$

 

 

1.3 밴디트 알고리즘

• 플레이어는 슬롯머신의 보상 기댓값 모름
  • → 실제 플레이 후 자신의 선택이 얼마나 좋았는지, 나빴는지 추정
  • → 슬롯머신의 가치를 추정하는 방법

 

 

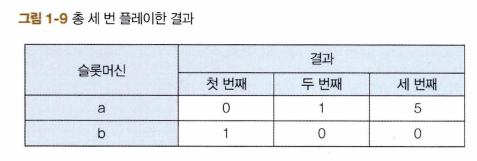
• 가치 추정 방법
  • 슬롯머신 a의 가치 추정치 $Q(a) = \frac{0 + 1 + 5}{3} = 2$
  • 슬롯머신 b의 가치 추정치 $Q(b) = \frac{1 + 0 + 0}{3} = 0.33..$
  • 표본 평균 sample mean
    • 슬롯머신을 실제로 플레이하여 얻은 보상은 어떤 확률 분포에서 생성된 샘플(표본)
    • 샘플링 횟수가 늘어날수록 실젯값(보상의 기댓값)에 가까워짐
• 평균을 구하는 코드
  • 보상 $R_1 + R_2 + \cdots + R_n$, n번 행동 → 행동 가치 추정치 $Q_n = \frac{R_1 + R_2 + \cdots + R_n}{n}$
  • 효율적으로 계산하려면
    • 매번 $R_1 + R_2 + \cdots + R_n$를 계산하는 것이 아닌
    • $Q_{n-1}$ 에서 $Q_n$으로 갱신될 때 $R_n - Q_{n-1}$ 의 길이에 $\frac{1}{n}$ 을 곱한만큼 이동
      • $\frac{1}{n}$ 이 갱신되는 양을 조정
      • $\frac{1}{n}$ : 학습률 learning rate 역할

Q = 0

for n in range(1, 11):
    reward = np.random.rand()
    Q = Q + (reward - Q) / n  # [식 1.5]
    print(Q)

 

• 증분 구현 incremental implementation: $Q_1, Q_2, Q_3 ...$ 식으로 하나씩 순차적으로 증가

 

• 플레이어의 정책
  • 탐욕 정책 greedy policy: 가치 추정치(실제 획득한 보상의 평균)가 가장 큰 슬롯머신을 선택하는 정책
    • 한계점: 가치 추정치 ‘불확실성’ → 최선의 행동 놓칠 수 있음
    • 불확실성을 줄여 추정치의 신뢰도를 높여야 함 → 활용, 탐색
    • 활용 exploitation: 지금까지 실제로 플레이한 결과를 바탕으로 가장 좋다고 생각되는 슬롯머신을 플레이 (탐욕 정책)
    • 탐색: exploration: 슬롯머신의 가치를 정확하게 추정하기 위해 다양한 슬롯머신을 시도
    • “활용과 탐색의 균형을 어떻게 잡느냐” → $\epsilon$-탐욕 정책 (엡실론-그리디 정책)
  • $\epsilon$-탐욕 정책
    • $\epsilon$의 확률 ($\epsilon$=0.1)로 ‘탐색’, 나머지는 ‘활용’ 하는 방식
      • 90%는 탐욕 선택, 10%는 랜덤 선택

 

1.4 밴디트 알고리즘 구현

• (단순화 설정)
  • 보상: 승리(1), 패배 (0)
  • 승리 확률이 설정되어 있다고 가정
  • 슬롯머신 총 10대
• 슬롯머신 구현
  • init 메서드: 각 머신 승률 무작위 설정
  • play: 몇 번째 슬롯머신 플레이 할지 결정, 현재 승률과 슬롯머신의 승률 비교 후 결과 반환

class Bandit:
    def __init__(self, arms=10):  # arms = 슬롯머신 대수
        self.rates = np.random.rand(arms)  # 슬롯머신 각각의 승률 설정(무작위)

    def play(self, arm):
        rate = self.rates[arm]
        if rate > np.random.rand():
            return 1
        else:
            return 0

 

• 에이전트 구현
  • action_size: 에이전트가 선택할 수 있는 행동의 가지 수 (지금 문제에서는 슬롯머신의 대수)
  • update 메서드: 슬롯머신의 가치 추정
  • get_action 메서드: $\epsilon$-탐욕 정책으로 행동을 선택하는 메서드
    • self.epsilon의 확률로 무작위 행동 선택 (=랜덤 탐색)
    • 그 외 (=활용, 탐욕)

class Agent:
    def __init__(self, epsilon, action_size=10):
        self.epsilon = epsilon  # 무작위로 행동할 확률(탐색 확률)
        self.Qs = np.zeros(action_size) # 각 슬롯머신의 가치 추정치
        self.ns = np.zeros(action_size) # 각 슬롯머신의 플레이 횟수

    # 슬롯머신의 가치 추정
    def update(self, action, reward):
        self.ns[action] += 1
        self.Qs[action] += (reward - self.Qs[action]) / self.ns[action]

    # 행동 선택(ε-탐욕 정책)
    def get_action(self):
        if np.random.rand() < self.epsilon:
            return np.random.randint(0, len(self.Qs))  # 무작위 행동 선택
        return np.argmax(self.Qs)  # 탐욕 행동 선택

 

• 실행
  • for 문 안에서 에이전트와 환경이 상호작용
  • 각 단계까지 얻은 보상의 합 → total_rewards 리스트에 추가
  • 그 동안의 승률 → rates 리스트에 추가

steps = 1000
epsilon = 0.1

bandit = Bandit()
agent = Agent(epsilon)
total_reward = 0
total_rewards = []  # 보상 합
rates = []          # 승률

for step in range(steps):
    action = agent.get_action()   # 1. 행동 선택
    reward = bandit.play(action)  # 2. 실제로 플레이하고 보상을 받음
    agent.update(action, reward)  # 3. 행동과 보상을 통해 학습
    total_reward += reward

    total_rewards.append(total_reward)       # 현재까지의 보상 합 저장
    rates.append(total_reward / (step + 1))  # 현재까지의 승률 저장

print(total_reward)

# [그림 1-12] 단계별 보상 총합
plt.ylabel('Total reward')
plt.xlabel('Steps')
plt.plot(total_rewards)
plt.show()

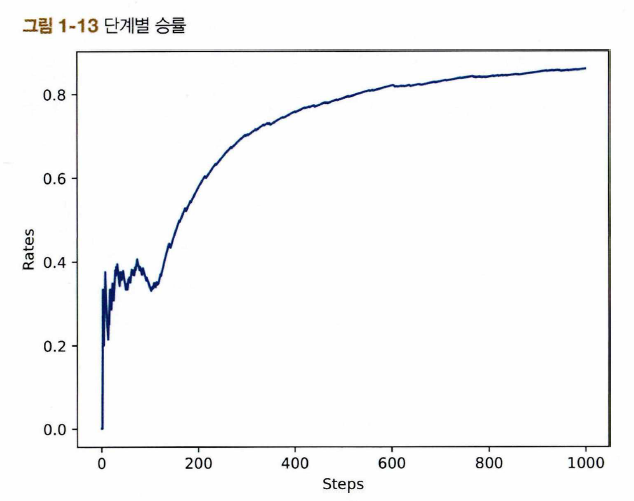
# [그림 1-13] 단계별 승률
plt.ylabel('Rates')
plt.xlabel('Steps')
plt.plot(rates)
plt.show()

 

• 실행 결과
  • 100 단계에서는 승률: 약 0.4
  • 500 단게 이후에는 완만
  • 최종 승률: 약 0.8 초과
  • → $\epsilon$-탐욕 정책 효과 있음!

 

 

• 알고리즘의 평균적인 특성
  • 같은 코드 10번 실행 시의 결과
  • → 강화 학습 알고리즘 비교 시, ‘무자위성’ 때문에 한 번의 실험만으로 판단하는 건 무의미
  • ‘평균적인 우수성’ 평가 필요

 

• $\epsilon$ 값 변경 시 결과
  • $\epsilon$ 를 0.01, 0.1, 0.3
  • $\epsilon$ = 0.3, 승률 빠르게 상승, 상승세 너무 완만 → 탐색을 과하게 시도
  • $\epsilon$ = 0.01, 꾸준한 상승, 상승 속도 느림 → 탐색 비율 너무 작음
  • → $\epsilon$ 로 “활용과 탐색의 균형” 조절

 

 

 

 

1.5 비정상 문제

• 정상 문제 stationary problem: 보상의 확률 분포가 변하지 않는 문제
  • 지금까지의 예제. 슬롯머신에 설정된 승률 고정
• 비정상 문제 non-stationary problem: 보상의 확률 분포가 변하도록 설정된 문제
• 비정상 문제의 슬롯머신

class NonStatBandit:
    def __init__(self, arms=10):
        self.arms = arms
        self.rates = np.random.rand(arms)

    def play(self, arm):
        rate = self.rates[arm]
        self.rates += 0.1 * np.random.randn(self.arms)  # 노이즈 추가
        if rate > np.random.rand():
            return 1
        else:
            return 0

 

• 비정상 문제를 풀기 위한 수식
  • 슬롯머신의 가치 추정 → 표본 평균 계산
  • $Q_n = \frac{R_1 + R_2 + \cdots + R_n}{n}
    = \frac{1}{n} R_1 + \frac{1}{n} R_2 + \cdots + \frac{1}{n} R_n$
  • $\frac{1}{n}$: 각 보상에 대한 ‘가중치’
    • 모든 보상에 똑같은 가중치 부여
    • 비정상 문제에는 비적합
    • 시간이 흐르면 환경(슬롯머신의 확률)이 변함
    • → 과거 데이터(보상)의 중요도는 점점 낮아져야 함, 최근 데이터 중요도 점점 커져야 함
  • 기존 행동 가치 추정치 $Q_n = Q_{n-1} + \frac{1}{n}(R_n - Q_{n-1})$
  • 비정상 행동 가치 추정치 $Q_n = Q_{n-1} + \alpha(R_n - Q_{n-1})$
    • $\alpha$ 라는 고정값, $0<\alpha<1$
    • 오래 전에 받은 보상일수록 가중치 작아짐
    • 기하급수적으로 작아짐 (지수적으로 감소, 지수 이동 평균, 지수 가중 이동 평균)

 

 

• 비정상 문제 구현
  • $\frac{1}{n}$ 대신 고정값 $\alpha$로 갱신
  • 결과
    • alpha const update가 고정값인 alpha로 갱신했을 때의 결과 (alpha=0.8)
    • → 고정값 갱신 결과가 훨씬 더 좋음

    class AlphaAgent:
      def __init__(self, epsilon, alpha, actions=10):
          self.epsilon = epsilon
          self.Qs = np.zeros(actions)
          self.alpha = alpha  # 고정값 α
    
      def update(self, action, reward):
          # α로 갱신
          self.Qs[action] += (reward - self.Qs[action]) * self.alpha
    
      def get_action(self):
          if np.random.rand() < self.epsilon:
              return np.random.randint(0, len(self.Qs))
          return np.argmax(self.Qs)