

활성화 함수
- 활성화 함수 Activation Function
- 인공 신경망에서 사용되는 은닉층을 활성화하기 위한 함수
- 활성화: 인공 신경망의 뉴런의 출력값을 선형에서 비선형으로 변환하는 것
- 네트워크가 데이터의 복잡한 패턴을 기반으로 학습하고 결정을 내릴 수 있게 제어함
- 가중치와 편향으로 이루어진 노드를 선형에서 비선형으로 갱신하는 역할
- 예) 출근 시간 예측 모델 구현
- 일어난 시간(x1), 기상 상태(x2)
- 기상 상태(x2)보다 일어난 시간(x1)이 더 영향력이 크다는 것을 직관적으로 알 수 있음
- → 연산 과정에서 일어난 시간(x1)은 더 많이 활성화(Activate)돼야 하며, 기상 상태(x2)는 비교적 비활성화(Deactivate)돼야 함
- 비선형 구조를 가져 역전파 과정에서 미분값을 통해 학습이 진행될 수 있게 함
- 활성화 함수가 선형 구조라면, 미분 과정에서 항상 상수가 나오므로 학습 진행이 어려움
- 활성화 함수는 입력을 정규화하는 과정으로 볼 수 있음
- 인공 신경망에서 사용되는 은닉층을 활성화하기 위한 함수
이진 분류
- 활성화 함수를 활용해 이진 분류 모델 예측 진행
- 이진 분류: 규칙에 따라 입력된 값을 두 그룹으로 분류하는 작업
- 참 또는 거짓으로 결과를 분류하기 때문에 논리 회귀(Logistic Regression) 또는 논리 분류(Logistic Classfication)라고 부름
- 관측치는 0~1 범위로 예측된 점수를 반환
- 데이터를 0 또는 1로 분류하기 위해 임계값을 0.5로 설정
- Y가 0.5보다 작은 값은 거짓, 0.5보다 큰 값은 참
- Y값이 0~1의 범위를 갖게 하기 위해 시그모이드 함수(Sigmoid Function)와 같은 활성화 함수를 적용함
시그모이드 함수
- S자형 곡선 모양
- 반환값은 0~1 또는 -1~1의 범위를 가짐
- 수식
- 시그모이드의 함수의 x의 계수: S자형 곡선의 경사 결정
- 계수가 0에 가까워질수록 완만한 경사
- 0에서 멀어질수록 급격한 경사
- 시그모이드의 함수의 x의 계수: S자형 곡선의 경사 결정
- $$
Sigmoid(x) = \frac{1}{1 + e^{-x}}
$$ - 주로 로지스틱 회귀에 사용됨
- 독립 변수(X)의 선형 결합을 활용하여 결과를 예측
- 로지스틱 회귀는 분류에서도 사용 가능
- 출력값이 0.5보다 낮으면 거짓으로 분류, 0.5보다 크면 참으로 분류
- 장점
- 유연한 미분값을 가짐. 입력에 따라 값이 급격하게 변하지 않는다는
- 출력값의 범위가 0~1사이로 제한 → 정규화 중 기울기 폭주(Exploding Gradient) 문제가 발생하지 않고 미분 식이 단순한 형태를 가짐
- 단점
- 기울기 소실(Vanishing Gradient) 문제 발생
- 신경망은 기울기를 이용해 최적화된 값을 찾아가는데, 계층이 많아지면 점점 값이 0에 수렴되는 문제가 발생해 성능이 떨어짐
- Y값의 중심이 0이 아님. 입력 데이터가 항상 양수라면, 기울기는 모두 양수 또는 음수가 되어 기울기가 지그재그 형태로 변동하는 문제점 발생 → 학습 효율성 감소
- 기울기 소실(Vanishing Gradient) 문제 발생
이진 교차 엔트로피
- 이진 분류에 비용 함수로 평균 제곱 오차를 사용하면 좋은 결과를 얻기 힘듦
- 예측값과 실제값의 값 차이가 작으면 계산되는 오차 또한 크기가 작아져, 학습 진행 어려움
- → 이진 교차 엔트로피 (Binary Cross Entropy, BCE)를 오차 함수로 사용
- 이진 교차 엔트로피
- 로그 함수를 활용해 오차 함수를 구현
- 두 가지 로그 함수를 교차해 오차를 계산

- 이미지 출처: https://velog.io/@zlddp723/머신러닝을-위한-기초수학-정보와-엔트로피-Shannon-크로스-엔트로피-Cross
- 기존의 평균 제곱 오차 함수는 명확하게 불일치하는 경우에도 높은 손실 값 반환 x
- → 로그 함수는 로그의 진수가 0에 가까워질수록 무한대로 발산하는 특정 = 불일치 비중이 높을수록 높은 손실 Loss 값 바낳놘
- 로그 함수의 경우 한쪽으로는 무한대로 이동, 다른 한쪽으로는 0에 가까워짐
- → 기울기가 0이 지점을 찾기 위해 두 가지 로그 함수를 하나로 합쳐 사용
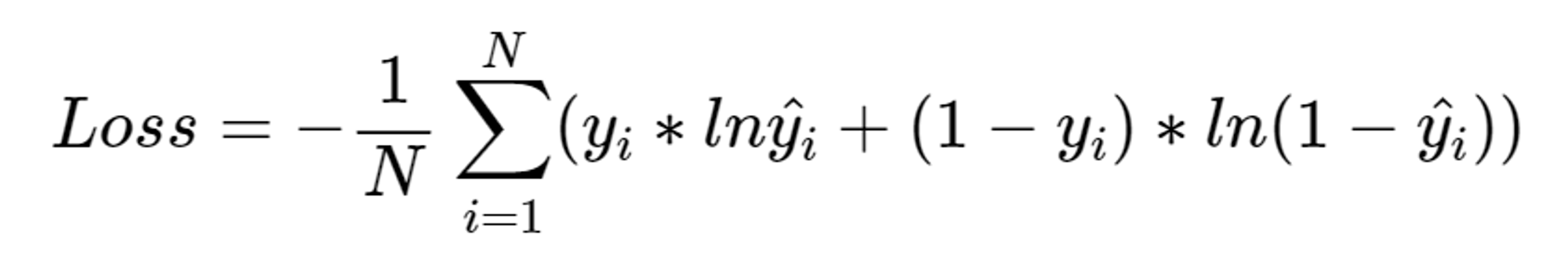
이진 분류: 파이토치
- 예제
- x, y, z와 pass의 관계: x, y, z가 모두 40 이상, 평균 60이상일 때 True 반환
- 사용자 정의 데이터세트
class CustomDataset(Dataset):
def __init__(self, file_path):
df = pd.read_csv(file_path)
self.x1 = df.iloc[:, 0].values
self.x2 = df.iloc[:, 1].values
self.x3 = df.iloc[:, 2].values
self.y = df.iloc[:, 3].values
self.length = len(df)
def __getitem__(self, index):
x = torch.FloatTensor([self.x1[index], self.x2[index], self.x3[index]])
y = torch.FloatTensor([int(self.y[index])])
return x, y
def __len__(self):
return self.length호출 메서드 __getitem__ : x는 입력값 (x1, x2, x3)을 할당하고, y는 실제값(y)를 반환
- 사용자 정의 모델
class CustomModel(nn.Module):
def __init__(self):
super().__init__()
self.layer = nn.Sequential(
nn.Linear(3, 1),
nn.Sigmoid()
)
def forward(self, x):
x = self.layer(x)
return x- Module 클래스를 상속받아 사용자 모델 정의
- super 함수를 통해 Module 클래스 초기화, 사용할 계층을 정의
- 시퀀셜 Sequential을 활용해 여러 계층을 하나로 묶음. 묶어진 계층을 순차적으로 실행됨. 가독성을 높임
- 선형 변환 함수의 입력 데이터 차원 크기(in_features)는 3을 입력
- 출력 데이터 차원 크기 (out_features)는 1을 입력
- 시그모이드 함수를 적용 예정. 시그 모이드 함수 (nn.Sigmoid)를 선형 변환 함수(nn.Linear) 뒤에 연결
- 이진 교차 엔트로피
criterion = nn.BCELoss().to(device)- 이진 교차 엔트로피 클래스(nn.BCELoss)로 criterion 인스턴스 생성
- 비용 함수로 criterion 인스턴스에서 순전파를 통해 나온 출력값과 실제값을 비교해 오차를 계산
- 기존 평균 제곱 오차 클래스(nn.MSELoss) 클래스와 동일한 방식으로 적용
비선형 활성화 함수
- 비선형 활성화 함수 Non-linear Activations Function
- 네트워크에 비선형성을 적용하기 위해 인공 신경망에서 사용되는 함수
- 입력이 단순한 선형 조합이 아닌 형태로 출력을 생성하는 함수를 의미
- 실제 세계의 입출력 관계가 대부분 비선형적인 구조를 갖고 있기 때문
- → 네트워크가 학습 데이터의 복잡한 패턴과 관계를 학습할 수 있게 지원
- 계단 함수 Step Function
- 이진 함수 Binary Activation Funcition이라고도 함
- 퍼셉트론 Perceptron에서 최초로 사용한 활성화 함수 (초기의 퍼셉트론 모델은 (0, 1 출력 등)간단한 원리에 기반하여 설계되었고, 당신에는 주로 선형적으로 분리 가능한 문제에 초점을 두었기 때문에)
- 입력값의 합이 임계값을 넘으면 출력이 1이 되고, 넘지 못하면 0을 출력
- 딥러닝 모델에서는 사용되지 않는함수
- 임계값에서 불연속점을 가지므로 미분이 불가능해 학습 진행 불가 (계단 함수를 사용하면, 미분값이 대부분의 구간에서 0이 되어, 가중치 업데이트가 제대로 이루어지지 않습니다.)
- 역전파 과정에서 데이터가 극단적으로 변경되기 때문에 적합 X

이미지 출처: https://nongnongai.tistory.com/51
- 임계값 함수 Threshold Function
- 임계값보다 크면 입력값(x)을 그대로 전달, 임계값보다 작으면 특정 값으로 변경
- 선형 함수와 계단 함수의 조합
- 출력이 0 또는 1인 이진 분류 작업을 위해 신경망에서 자주 사용되는 효과적인 활성화 함수
- 입력에 대한 함수의 기울기 계산 불가 → 네트워크 최적화 어려움 → 사용 x (특별한 경우만 사용)
- 시그모이드 함수 Sigmoid Function
- 모든 입력값을 0과 1 사이의 값으로 매핑
- 이진 분류 신경망의 출력 계층에서 활성화 함수로 사용됨
- 단순한 형태의 미분식을 가짐
- 입력값에 따라 출력값이 급격하게 변하지 않음
- 출력값이 0~1범위 가짐 = 기울기 폭주 현상 방지 가능
- 출력값이 0~1 범위를 가지는 만큼 매우 큰 입력값이 입력돼도 최대 1의 값을 가지게 되어 기울기 소실이 발생
- 출력값의 중심이 0이 아니므로, 입력 데이터가 항상 양수인 경우에, 기울기는 모두 양수 또는 음수가 되어 기울기가 지그재그 형태로 변동하는 문제 발생 → 학습 효율성 감소
- 인공신경망은 기울기를 이용해 최적화된 값을 찾아가는데, 계층이 많아지면 점점 값이 0에 수렴하는 문제 발생 → 시그모이드 함수는 은닉층에서는 활성화 함수로 사용되지 x, 주로 출력층에서만 사용됨
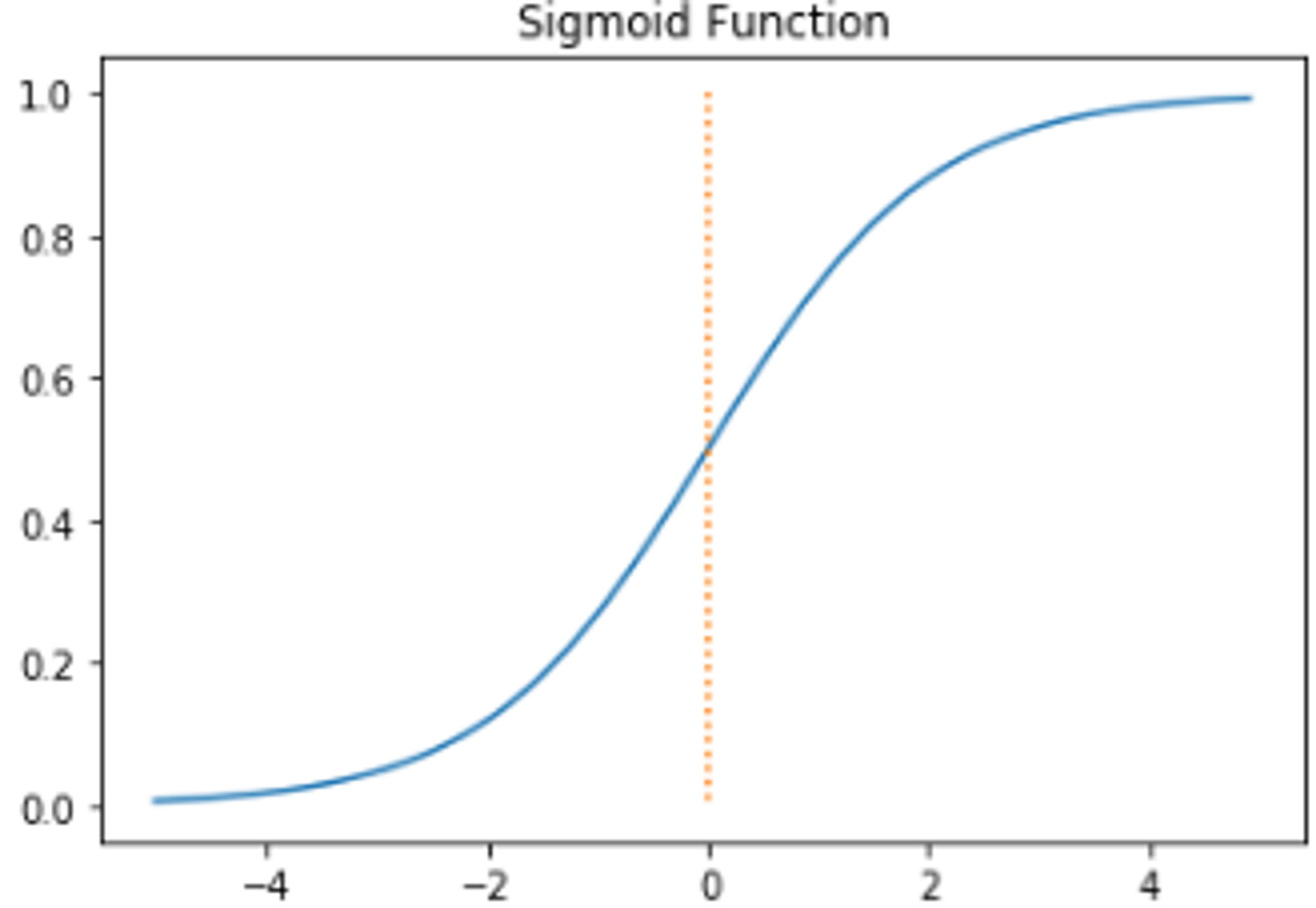
이미지 출처: https://wikidocs.net/60683
- 하이퍼볼릭 탄젠트 함수 Hyperbolic Tangent Function
- 시그모이드 함수와 유사한 형태, 출력값의 중심이 0이다.
- 출력값이 -1~1의 범위, 시그모이드에서 발생하지 않는 음수 값 반환 가능
- 기울기 소실이 비교적 덜 발생 (출력값의 범위가 더 넓고 다양한 형태로 활성화 가능)
- 입력값 x이 4보다 큰 경우 출력값이 1에 수렴. 동일하게 기울기 소실이 발생

- 이미지 출처: https://wikidocs.net/60683
- ReLU 함수 Rectified Linear Unit Function
- 0보다 작거나 같으면 0을 반환, 0보다 크면 선형 함수에 값을 대입하는 구조
- 선형 함수에 대입하기 때문에, 입력값이 양수라면 출력값이 제한 되지 않아 기울기 소실이 발생하지 않음
- 수식 또한 매우 간단해, 순전파나 역전파 과정의 연산이 매우 빠름
- 입력값이 음수인 경우 항상 0을 반환, 가중치나 편향이 갱신되지 않을 수 있음
- 가중치의 합이 음수가 되면 해당 노드는 더 이상 값을 갱신하지 않아 죽은 뉴런 (Dead Neuron, Dying ReLU)이 됨
- 딥러닝 네트워크에서 널리 사용되는 활성화 함수

이미지 출처: https://wikidocs.net/60683
- LeakyReLU 함수 Leaky Recified Linear Unit Function
- 음수 기울기를 제어, 죽은 뉴런 현상 방지하기 위해 사용
- 양수인 경우 ReLU 함수와 동일, 음수인 경우 작은 값이라도 출력시켜 기울기를 갱신하게 함
- 작은 값을 출력시키면 더 넓은 범위의 패턴을 학습할 수 있어 네트워크의 성능을 향상시키는 데 도움

이미지 출처: https://wikidocs.net/60683
- PReLU 함수 Parametric Rectified Linear Unit Function
- LeakyReLU 함수와 형태가 동일하지만, 음수 기울기 값을 고정값이 아닌, 학습을 통해 갱신되는 값으로 간주함
- 음수 기울기는 지속해서 값이 변경됨
- 값이 지속해서 갱신되는 매개변수이므로, 학습 데이터세트에 영향을 받음
- ELU 함수 Exponential Linear Unit Function
- 지수 함수를 사용하여 부드러운 곡선의 형태를 가짐
- 기존 ReLU함수와 ReLU 변형 함수는 0에서 끊어지는데, ELU함수는 음의 기울기에서 비선형 구조를 가짐
- → 입력값이 0인 경우에도 출력값이 급변하지 않아, 경사 하강법의 수렴속도가 비교적 빠름.
- 더 복잡한 연산을 진행하기 때문에, 학습 속도는 느림
- 수렴 속도: 몇 번의 학습으로 최적화된 값을 찾는가를 의미
- 학습 속도: 학습이 완료되기까지의 전체 속도를 의미
- 데이터의 복잡한 패턴과 관계를 학습하는 네트워크의 능력을 향상시키는 데 도움됨

- 이미지 출처: https://deeesp.github.io/deep learning/DL-Activation-Functions/
- 소프트맥스 함수 Softmax Function
- 차원 벡터에서 특정 출력값이 k번째 클래스에 속할 확률을 계산
- 클래스에 속할 확률을 계산하는 활성화 함수
- 은닉층에서 사용하지 않고, 출력층에서 사용
- 네트워크의 출력을 가능한 클래스에 대한 확률 분포로 매핑
- 이 외에도 소프트민 함수 Softmin Function, 로그 소프트맥스 함수 Log Softmax Function 등이 있음
'Theory > Pytorch' 카테고리의 다른 글
| [파이토치 트랜스포머 #7] 4장 파이토치 심화 - 1) 과대적합과 과소적합, 배치 정규화 (0) | 2024.04.12 |
|---|---|
| [파이토치 트랜스포머 #6] 3장 파이토치 기초 - 6) 순전파와 역전파, 퍼셉트론 (1) | 2024.04.03 |
| [파이토치 트랜스포머 #5] 3장 파이토치 기초 - 4) 모델/데이터세트 분리, 모델 저장 및 불러오기 (0) | 2024.03.06 |
| [파이토치 트랜스포머 #4] 3장 파이토치 기초 - 3) 데이터세트와 데이터로더 (1) | 2024.03.06 |
| [파이토치 트랜스포머 #3] 3장 파이토치 기초 - 2) 가설, 손실함수, 최적화 (2) | 2024.03.04 |



