

순전파와 역전파
- 순전파 Forward Propagation
- 순방향 전달 Forward Pass라고도 하며, 입력이 주어지면 신경망의 출력을 계산하는 프로세스
- 입력 데이터를 기반으로 신경망을 따라 입력층부터 출력층가지 차례대로 변수를 계산하고 추론한 결과를 전달
- 네트워크에 입력값(x)을 전달해 순전파 연산을 진행
- 계층마다 가중치와 편향으로 계산된 값이 활성화 함수에 전달
- 활성화 함수에서 출력값 (y 햇)이 계산되고 이 값을 손실함수에 실젯값(y)과 함께 연산해 오차 계산
- 역전파 Back Propagation
- 순전파 방향과 반대로 연산 진행
- 순전파와 역전파는 네트워크가 입력값을 기반으로 예측을 수행할 수 있게 함
- 학습을 반복할수록 모델의 성능 향상 가능
- 신경망 학습에서 중요 프로세스 중 하나
유튜브 참고하여 개념 정리
https://www.youtube.com/watch?v=1Q_etC_GHHk&t=242s
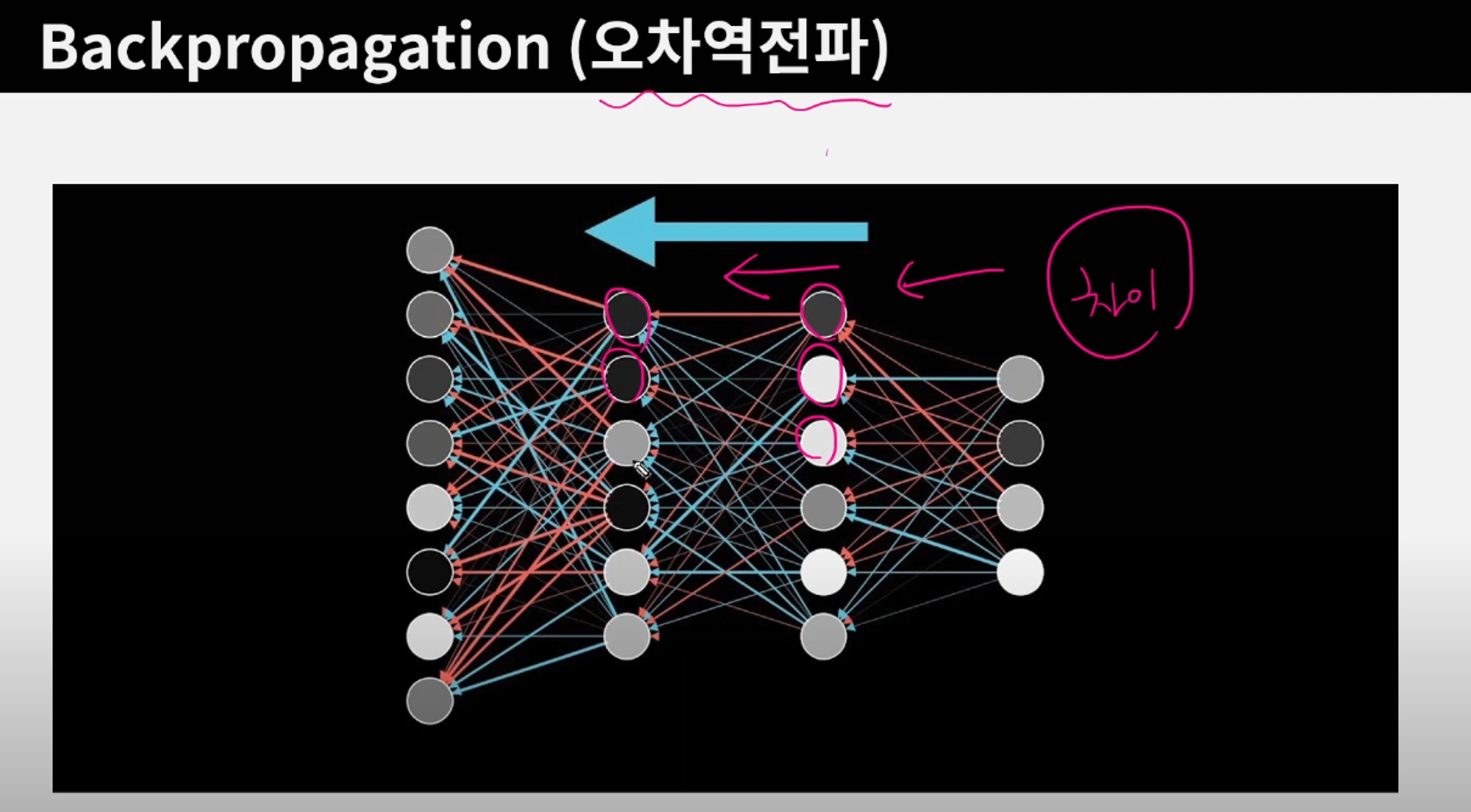
- 내가 예측하고자 하는 [타겟값]과 모델의 [예측값]이 얼마나 차이가 있는지 계산 → 뒤로 전파해 나가면서 각 노드가 가진 가중치를 업데이트(갱신) 시키는 과정
- 순전파 Foward Pass
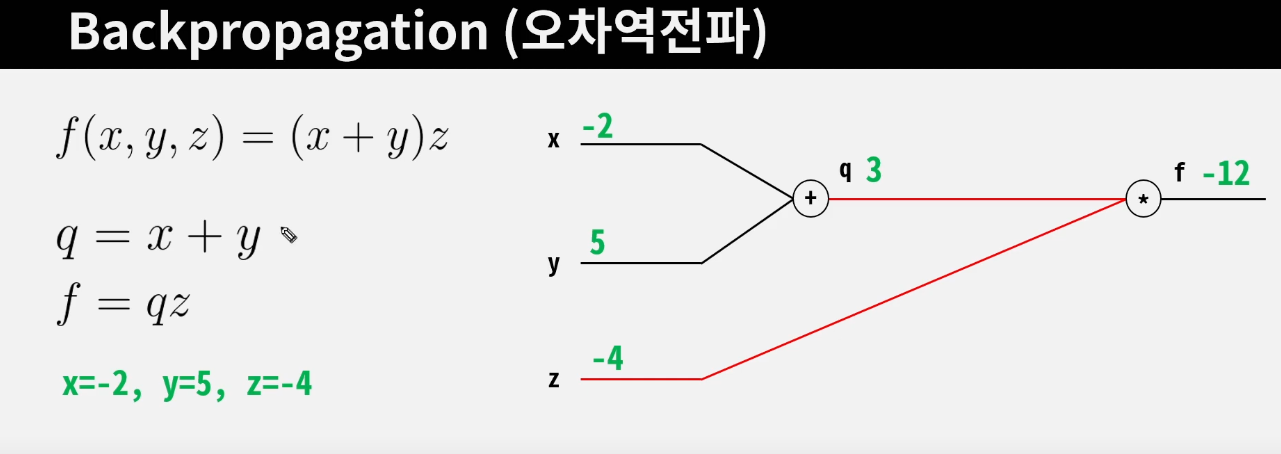
- q에 대한 x의 미분값, q에 대한 y의 미분값를 구함

- f에 대한 q의 미분값, f에 대한 z의 미분값를 구함

- 궁극적으로 구하려고 하는것: f에 대한 x, y의 미분값
- x, y가 1만큼 변했을 때 f의 변화량
- Chain Rule을 사용
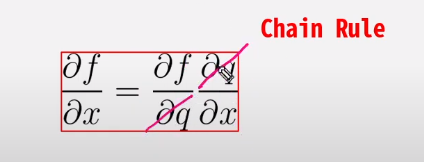


-
- Local Gradient, Global Gradient
- Forward Pass 시 우리는 Local Gradient를 미리 구하여 저장할 수 있음
- Global Gradient는 역으로 계산되면서 내려옴
- Loss에 대한 x의 값을 구할 때
- 전 단계의 Global Gradient만 있으면 Loss의 x에 대한 편미분한 값을 구할 수 있음
- Chain Rule을 활용하여 Local Gradient * Global Gradient 곱하여 계산
- Local Gradient, Global Gradient

갱신 결과 비교
- 머신러닝은 가중치와 편향 갱신을 반복하면서 최적의 가중치와 편향을 찾음
- 특정한 횟수에 도달할 때까지 연산을 진행하거나 오찻값이 일정 이하로 떨어지게 되면 학습을 종료
- 오차 함수나 활성화 함수가 다르면 다른 결과값을 얻음
- 시그모이드
- 출력값의 범위를 0~1사이로 제한, 역전파 과정에서 0에 가까운 기울기가 곱해짐 (성능 저하)
- 출력층에 가까운 레이어의 변화량은 커지고, 입력층에 가까운 레이어의 변화량은 작아짐
- → 깊은 모델의 은닉층에서는 시그모이드를 활성화 함수로 사용하지 않음
- 시그모이드
퍼셉트론
- 인공 신경망의 한 종류
- 출력이 0 또는 1인 작업을 의미하는 이진 분류 작업에 사용되는 간단한 모델
- 신경 세포 (Neuron)가 신호를 전달하는 구조와 유사한 방식으로 구현됨
- TLU (Threshold Logic Unit) 형태 기반
- 계단 함수를 적용해 결과를 반환
- 생물학적 신경망

- 이미지 출처: 나무위키
- 가지돌기(수상돌기)가 외부의 신경 자극을 받아 신경세포체에서 가중 압력을 받아 신호를 전달
- 전달되는 신호는 축삭을 통해 다른 신경 세포로 최종 신호를 전달함
- 신경 세포에서 다른 신경 세포로 신호를 전달할 때 시냅스라는 연결 부위를 통해 신호를 전달
- 전달되는 신호를 어느 정도의 세기로 전달할지 결정
- 퍼셉트론
- 가지돌기는 입력값(x)을 전달받음
- 신경세포체는 입력값(x)을 토대로 특정 연산 진행 → 임계값보다 크면 전달, 작으면 전달x
- 시냅스는 여러 퍼셉트론을 연결
- 많은 머신러닝 애플리케이션에서 사용됨
- 이진 분류 작업에서 여전히 많이 사용되는 간단하고 효율적인 모델
- 제한 사항 존재
- 복잡한 작업에 더 적합한 고급 신경망 모델 개발됨
단층 퍼셉트론
- Single Layer Perceptron
- 하나의 계층을 갖는 모델을 의미
- 입력을 통해 데이터가 전달, 입력값(x)은 각각의 가중치와 함께 노드에 전달
- 전달된 입력값과 가중치를 곱한 값이 활성화 함수에 전달
- 활성화 함수에서 출력값 $\hat{y}$ 이 계산되고, 이 값을 손실 함수에 실젯값 y과 함께 연산, 가중치 변경

이미지 출처: https://hyeonjiwon.github.io/artificial intelligence/AI-3/
- 단층 퍼셉트론 한계
- AND, OR, NAND 게이트와 같은 구조를 갖는 모델 쉽게 구현 가능
- XOR 게이트처럼 하나의 기울기로 표현하기 어려운 구조에서는 적용 불가

이미지 출처: https://wikidocs.net/60680
다층 퍼셉트론
- Multi-Layer Perceptron, MLP
- 단층 퍼셉트론을 여러 개 쌓아 은닉층을 생성, 은닉층이 한 개 이상인 퍼셉트론 구조
- 심층 신경망(Deep Neural Network, DNN): 은닉층을 2개 이상 연결
- 은닉층이 늘어날수록 더 복잡한 구조의 문제 해결 가능
- 계층이 늘어날수록 갱신해야하는 가중치나 편향 증가 = 많은 학습 데이터와 연산량 필요
- 다층 퍼셉트론의 학습 방법 (순전파, 역전파)
- 입력층부터 출력층까지 순전파 진행
- 출력값(예측값)과 실젯값으로 오차 계산
- 오차를 퍼셉트론의 역방향으로 보내면서 입력된 노드의 기여도 측정
- 손실 함수를 편미분해 기울기 계산
- Chain Rule을 통해 기울기 계산
- 입력층에 도달할 때까지 노드의 기여도 측정
- 모든 가중치에 최적화 알고리즘 수행
'Theory > Pytorch' 카테고리의 다른 글
| [파이토치 트랜스포머 #8] 4장 파이토치 심화 - 2) 가중치 초기화 (0) | 2024.04.12 |
|---|---|
| [파이토치 트랜스포머 #7] 4장 파이토치 심화 - 1) 과대적합과 과소적합, 배치 정규화 (0) | 2024.04.12 |
| [파이토치 트랜스포머 #6] 3장 파이토치 기초 - 5) 활성화 함수 (1) | 2024.03.17 |
| [파이토치 트랜스포머 #5] 3장 파이토치 기초 - 4) 모델/데이터세트 분리, 모델 저장 및 불러오기 (0) | 2024.03.06 |
| [파이토치 트랜스포머 #4] 3장 파이토치 기초 - 3) 데이터세트와 데이터로더 (1) | 2024.03.06 |



