

정칙화
- 정칙화 Regularization
- 모델 학습 시 발생하는 과대적합을 방지하기 위해 사용되는 기술
- 모델이 암기가 아니라 일반화할 수 있도록 손실함수에 규제 Penalty를 가하는 방식
- 암기 Memorization란
- 모델이 데이터의 일반적인 패턴을 학습하는 것이 아니라 훈련 데이터의 노이즈나 패턴을 학습한 것
- 일반화 Generalization 란
- 특정 데이터가 갖고 있는 노이즈를 학습하는 것이 아닌, 데이터의 일반적인 패턴을 학습하는 것
- 손실 함수에 규제를 가해 모델의 일반화 성능을 향상
- 학습 데이터들이 갖고 있는 작은 차이점에 대해 덜 민감해져서 모델의 분산 값이 낮아짐
- 모델이 학습 시 의존하는 데이터의 특징 수 감소 → 모델의 추론 능력 개선
- 모델이 비교적 복잡하고 학습에 사용되는 데이터가 적을 때 활용
- 이미 정규화 되어 있는 경우에는 사용하지 않아도 됨
- 종류
- L1 정칙화, L2 정칙화, 가중치 감쇠, 드롭아웃 등
L1 정칙화
- L1 정칙화(L1 Regularization): 라쏘 정칙화(Lasso Regularization)라고도 불림
- L1 노름(L1 Norm) 방식 사용해 규제
- 벡터 또는 행렬값의 절댓값 합계 계산
- 손실 함수에 가중치 절댓값의 합을 추가해 과대적합 방지
- 모델은 가중치 절댓값의 합도 최소가 되는 방향으로 학습 진행 (원래도 모델은 비용이 0이 되는 방향으로 진행되기 때문에)
- 모델 학습 시 값이 크지 않은 가중치들은 0으로 수렴
- 예측에 필요한 특징의 수를 줄임 = 특징 선택 효과
- 수식
- $\lambda$ : 규제 강도. 너무 많거나 적은 규제를 가하지 않게 조절하는 하이퍼 파라미터
- 0보다 큰 값
- 규제 강도가 0에 가까워질수록 모델은 더 많은 특징 사용→ 과대적합에 민감해짐
- 너무 높이면 대부분의 가중치가 0에 수렴하여 과소적합 문제 발생 가능
- $\lambda$ : 규제 강도. 너무 많거나 적은 규제를 가하지 않게 조절하는 하이퍼 파라미터
- $$
\text{L}1 = \lambda \sum{i=0}^{n} |\omega_i|
$$ - 모델의 가중치를 정확히 0으로 만드는 경우가 있기 때문에 희소한 모델이 될 수 있음
- 예측에 사용되는특징의 수가 줄어들게 되므로 정보 손실 발생 가능
- L1 정칙화를 적용하는 경우, 입력 데이터에 더 민감해지며, 항상 최적의 규제를 하는 것이 아니기에 주의 필요
- L1 노름(L1 Norm) 방식 사용해 규제
- 예시 코드
- 모델의 가중치를 모두 계산해 모델을 갱신 → 계산 복잡도를 높임
- L1 정칙화는 미분 불가 → 역전파 계산 시 더 많은 리소스 소모
- 하이퍼파라미터인 _lamda 값이 적절하지 않은 경우 → 여러 번 반복해 최적의 _lamda 값 찾아야함
for x, y in train_dataloader:
x = x.to(device)
y = y.to(device)
output = model(x)
_lambda = 0.5
l1_loss = sum(p.abs().sum() for p in model.parameters())
loss = criterion(output, y) + _lambda * l1_loss- L1 정칙화는 주로 선형 모델에 적용
- 선형 회귀 모델에 L1 정칙화를 적용하는 것 = 라쏘 회귀 Least Absolute Shrinkage and Selection Operator Regression
L2 정칙화
- L2 정칙화(L2 Regularization): 릿지 정칙화(Ridge Regularization)라고도 불림
- L2 노름(L2 Norm) 방식 사용해 규제
- 벡터 또는 행렬 값의 크기를 계산
- 손실 함수에 가중치 제곱의 합을 추가해 과대적합 방지
- 하나의 특징이 너무 중요한 요소가 되지 않도록 규제
- 모델 학습 시 오차를 최소화하면서 가중치를 작게 유지하고 골고루 분포되게끔 함 → 모델의 복잡도가 일부 조정
- 수식
- $$
\text{L}2 = \lambda \sum{i=0}^{n} \omega_i^2
$$ - (L1 정칙화 비교)
- (L2) 가중치 값들이 비교적 균일하게 분포
- (L2) 가중치를 0으로 만들지 않고 0에 가깝게 만듦
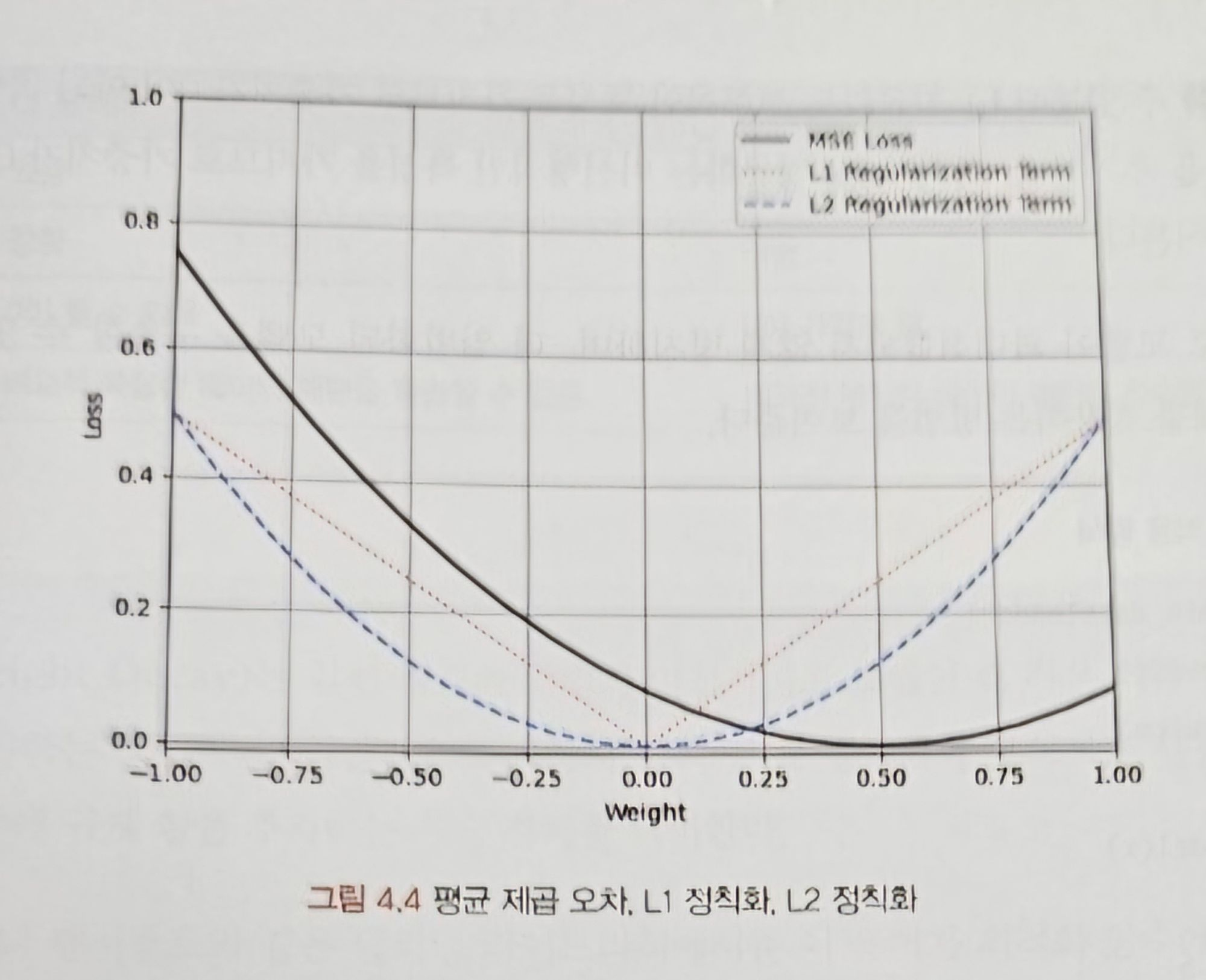
- $y=w×x$ 일 때,
- 가중치가 0.5가 실젯값, 규제 강도 0.5 → $y=0.5x$
- L1 정칙화는 가중치 절대값으로 계산 → 가중치가 0에 가까워질수록 선형적인 구조
- L2 정칙화는 가중치 제곱으로 계산 → 비선형적인 구조

- 가중치별로 정칙화를 적용한 손실 값
- L1 정칙화: 선형적인 특징 → 가중치가 0이 아닌 곳에서 모든 값에 고정적인 값을 추가
- L2 정칙화: 비선형적인 특징 → 0에 가까워질수록 규젯값이 감소
- 가중치별로 정칙화를 적용한 손실 값
- L2 노름(L2 Norm) 방식 사용해 규제
- 예시 코드
- (L1정칙화와 동일) 모델의 가중치를 모두 계산해 모델을 갱신 → 계산 복잡도를 높임
- 과대적합 방지를 위해, 조기 중지 또는 드롭아웃과 같은 기술과 함께 사용
- L2 정칙화는 주로 심층 신경망에서 사용함
- 선형 회귀 모델에서 L2 정칙화를 사용하는 경우 → 릿지 회귀 Ridge Regression
- 비교
| | L1 정칙화 | L2 정칙화 |
| --- | --- | --- |
| 계산 방식 | 가중치 절댓값의 합 | 가중치 제곱의 합 |
| 모델링 | 희소함 | 희소하지 않음 |
| 특징 선택 | 있음 | 없음 |
| 이상치 | 강함 | 약함 |
| 가중치 | 0이 될 수 있음 | 0에 가깝게 됨 |
| 학습 | 비교적 복잡한 데이터 패턴 학습 불가 | 비교적 복잡한 데이터 패턴 학습 가능 |가중치 감쇠
- 가중치 감쇠 Weight Decay
- (정칙화와 동일) 모델이 더 작은 가중치를 갖도록 손실 함수에 규제
- 일반적으로 L2 정칙화와 동의어로 사용되지만, 가중치 감쇠는 손실 함수에 규제 항을 추가하는 기술 자체를 의미
- 파이토치의 가중치 감쇠는 L2 정칙화와 동일, 최적화 함수에서 weight_decay 하이퍼파라미터를 설정해 구현, 조기 중지 또는 드랍아웃과 같은 기술과 함께 사용
optimizer = torch.optim.SGD(model.parameters(), lr=0.01, weight_decay=0.01)모멘텀
- 모멘텀 Momentum
- 경사 하강법 알고리즘의 변형 중 하나
- 이전에 이동했던 방향과 기울기의 크기를 고려해 가중치를 갱신
- 이를 위해, 지수 가중 가중 이동평균을 사용, 이전 기울기 값의 일부를 현재 기울기 값에 추가해 가중치를 갱신
- 이전 기울기 값에 의해 설정된 방향으로 더 빠르게 이동, 일종의 관성(Momentum) 효과를 얻음
- (가중치 감쇠 적용 방법과 동일) 최적화 함수의 momentum 하이퍼파라미터를 설정해 구현
- 수식
- vi 는 i번째 모멘텀 값, 이동 벡터를 의미. 이전 모멘텀 값 vi-1에 모멘텀 계수 $\gamma$를 곱한 값과 경사 하강법의 갱신 값의 합으로 계산됨
- $\gamma$는 하이퍼파라미터, 모멘텀 계수를 의미. 0~1 사이의 값. 일반적으로는 0.9와 같은 값 사용
- vi는 가중치 갱신을 위한 방향과 크기를 결정.
- 이전 기울기 값이 크면 모멘텀 계수에 의해 현재 기울기 값에 반영되므로 더 빠르게 수렴
- 모멘텀 계수가 0이면 경사하강법 수식과 동일
v_i = \gamma v_{i-1} + \alpha \nabla f(W_{i})
$$
$$
W_{i+1}= W_{i} - v_i
$$
엘라스틱 넷
- 엘라스틱 넷 Elastic-Net
- L1 정칙화와 L2 정칙화를 결합해 사용하는 방식
- 두 정칙화 방식의 선형 조합으로 사용하며 혼합 비율을 설정해 가중치를 규제
- 혼합 비율은 $\alpha$로 어떤 정칙화를 더 많이 반영할지 설정. 0~1 사이의 값.
- L1, L2 정칙화보다 트레이드오프 문제를 더 유연하게 대처 가능
- 특징의 수가 샘플의 수보다 더 많을 때 유의미한 결과.
- 상관관계가 있는 특징 더 잘 처리 가능
- 더 많은 튜닝, 계산 복잡도 → 많은 리소스 소모
- 수식
- $$
Elastic-Net = \alpha × L_{1} + (1-\alpha) × L_{2}
$$
드롭아웃
- 드롭아웃 Dropout
- 모델의 훈련 과정에서 일부 노드를 일정 비율로 제거하거나 0으로 설정해 과대적합을 방지하는 간단하고 효율적인 방법
- 동조화 현상 방지, 노드 간 의존성 억제에 효과
- 동조화 Co-adaption 현상
- 모델 학습 중 특정 노드의 가중치나 편향이 큰 값을 갖게 되면 다른 노드가 큰 값을 갖는 노드에 의존하는 것
- 과대적합을 발생시키는 이유 중 하나
- 특정 노드에 의존성이 생겨 학습 속도가 느려지고 새로운 데이터를 예측하지 못해 성능 저하 발생 가능
- 동조화 Co-adaption 현상
- 모델이 일부 노드를 제거해 학습하므로 투표Voting 효과를 얻을 수 있어 모델 평균화 Model Averaging 됨
- 드롭아웃 마스크를 사용해 모델을 여러 번 훈련 필요 → 훈련 시간 증가
- 데이터세트가 많지 않다면 효과 얻기 힘듦. 균일 학습 불가 → 성능 저하 발생 가능
- 충분한 데이터 세트와 비교적 깊은 모델에 적용

이미지 출처: https://thebook.io/080289/0604/
- 코드
- 신경망 패키지에 있는 Dropout 클래스로 쉽게 구현
- p 매개변수: 베르누이 분포 Bernoulli Distribution 의 모수
- 이 분포로 각 노드의 제거 여부를 확률적으로 선택
- 순방향 메서드에서 드롭아웃을 적용할 계층 노드에 적용
from torch import nn
class Net(nn.Module):
def __init__(self):
super().__init__()
self.layer1 = nn.Linear(10, 10)
self.dropout = nn.Dropout(p=0.5)
self.layer2 = nn.Linear(10, 10)
def forward(self, x):
x = self.layer1(x)
x = self.dropout(x)
x = self.layer2(x)
return x- (일반적으로) 배치 정규화와 동시에 사용 x, 다른 기법을 동시에 적용할 때 주의해 적용
- 배치 정규화와 드롭아웃은 서로의 정칙화 효과 방해 가능
- 배치 정규화의 경우 내부 공변량 변화를 줄여 과대적합 방지, 드롭아웃은 일부 노드 제거
- 동시 사용 시, 순방향 과정에서 다른 활성화 분포를 사용 → 훈련 과정 성능 저하 및 불안정
- (동시 사용 시) 드롭 아웃, 배치 정규화 순
- 드롭 아웃은 모델이 학습할 때만 적용. 추론 과정에서는 일부 노드 삭제x, 모든 노드 사용해 예측
- 극단적인 비율로 모델에 적용하지 않으면 일반적으로 성능 향상됨
- 비교적 많은 특징을 사용해 학습하는 이미지 인식, 음성 인식 모델에서 성능 향상 결과
그레이디언트 클리핑
- 그레이디언트 클리핑 Gradient Clipping
- 모델을 학습할 때 기울기가 너무 커지는 현상을 방지하는 데 사용되는 기술
- 과대 적합 모델: 특정 노드의 가중치가 너무 큼 → 높은 가중치: 높은 분산 값 → 모델 성능 저하
- 가중치 최댓값을 규제해 최대 임계값을 초과하지 않도록 기울기를 잘라 Clipping 설정한 임계값으로 변경
- 수식
- 가중치 노름이 최대 임계값 $\gamma$보다 높은 경우에 수행
- 기울기 벡터의 방향 유지, 기울기를 잘라 규제
- (일반적으로) L2 노름을 사용해 최대 기울기를 규제
- 최대 임계값 $\gamma$: 하이퍼파라미터, 사용자가 최대 임계값 설정. 0.1이나 1과 같이 작은 크기의 임계값을 적용하며 학습률을 조절하는 것과 비슷한 효과를 얻을 수 있음
- $$
\text{if } |\nabla J(\theta)| > \gamma
$$ - $$
\omega = \frac{\gamma \times \omega} {\|\omega\|}
$$
- 가중치 노름이 최대 임계값 $\gamma$보다 높은 경우에 수행
- 모델을 학습할 때 기울기가 너무 커지는 현상을 방지하는 데 사용되는 기술
- 가중치 값에 대한 엄격한 제약 조건을 요구하는 상황이거나 모델이 큰 기울기에 민감한 상황에서 유용하게 활용
- 순환 신경망 RNN이나 LSTM 모델 학습하는데 주로 사용됨
- 두 모델은 기울기 폭주에 취약
- 그레이디언트 클리핑은 최댓값을 억제 → 효과적
- 그레이디언트 클리핑 함수
- 기울기를 정규화하려는 매개변수 parameters 를 전달, 최대 노름 max_norm을 초과하는 경우 기울기 잘라냄
- 노름 유형 norm_type: 클리핑을 계산할 노름 유형 설정
- 무한대로 적용한다면 float(’inf’)로 설정
- 매개변수 기울기의 전체 노름 단일 벡터 grad_norm 반환
- 정규화된 기울기는 반환하지 않고 매개변수를 직접 수정
- 순환 신경망 RNN이나 LSTM 모델 학습하는데 주로 사용됨
grad_norm=torch.nn.utils.clip_grad_norm(
parameters,
max_norm,
norm_type=2.0
)- 코드
- 역전파 loss.backward를 수행한 이후 최적화 함수 optimizer.step를 반영하기 전에 호출
- 모델의 매개변수와 임계값을 인수로 사용하고 임계값을 초과하는 경우 기울기를 임계값으로 자르기 때문에 해당 구문 사이에 사용됨
- 모델 매개변수의 최댓값을 규제 → 매개변수는 model.parameters()를 입력, 최대 노름은 0.1이나 1과 같은 작은 값을 할당
for x, y in train_dataloader:
x = x.to(device)
y = y.to(device)
output = model(x)
loss = criterion(output, y)
optimizer.zero_grad()
loss.backward()
torch.nn.utils.clip_grad_norm_(model.parameters(), 0.1)
optimizer.step()- 기울기 최댓값을 규제해 비교적 큰 학습률 사용
- 최대 임곗값이 높으면 모델의 표현력이 떨어짐, 낮은 경우 오히려 학습 불안정 발생 가능
- 최대 임계값은 하이퍼파라미터이므로 값을 설정할 때 여러 번 실험하여 신중히 선택 필요
'Theory > Pytorch' 카테고리의 다른 글
| [파이토치 트랜스포머 #11] 4장 파이토치 심화 - 5) 사전 학습된 모델 (1) | 2024.07.03 |
|---|---|
| [파이토치 트랜스포머 #10] 4장 파이토치 심화 - 4) 데이터 증강 및 변환 (3) | 2024.06.30 |
| [파이토치 트랜스포머 #8] 4장 파이토치 심화 - 2) 가중치 초기화 (0) | 2024.04.12 |
| [파이토치 트랜스포머 #7] 4장 파이토치 심화 - 1) 과대적합과 과소적합, 배치 정규화 (0) | 2024.04.12 |
| [파이토치 트랜스포머 #6] 3장 파이토치 기초 - 6) 순전파와 역전파, 퍼셉트론 (1) | 2024.04.03 |



