[논문 읽기 #1]Spikelet: An Adaptive Symbolic Approximation for Finding Higher-Level Structure in Time Series

 

안녕하세요, 기존에 읽었던 논문들 & 정리해놨던 ppt를 오늘부터 조금씩 업로드하려고 합니다.

다소 이해가 부족할 수 있습니다...!(정독하는 모든 논문을 다 업로드할 예정은 아니고, ppt로 만들어둔 논문만 올리려구 합니당.. ㅎㅎ)

 

 

논문 기본 정보

 

Spikelet: An Adaptive Symbolic Approximation for Finding Higher-Level Structure in Time Series

• 2021 ICDM (IEEE International Conference on Data Mining)
• 후속 논문
  • Parameter free Spikelet Discovering Different Length and Warped Time Series Motifs using an Adaptive Time Series Representation
  • 2023 KDD
• 키워드: Time series, Time series Motifs, Adaptive Representation

 

 

 

Introduction

• Time series motif
  • 반복되는 subsequence구간, 중요한 패턴
  • Time series data mining에 중요
• 기존 연구 한계
  • 모티브 (문자로 표현), 의미론적 유사성 semantic similarity 발견 불가
    • 문자 그대로의 일치를 찾는 것으로 제한
• Spikelet
  • 스파이크 모양의 하위 시퀀스의 집합으로 시계열을 표현
  • 스파이크
    • 시계열 중 튄 부분 (추후 설명)

 

 

 

 

Related Works

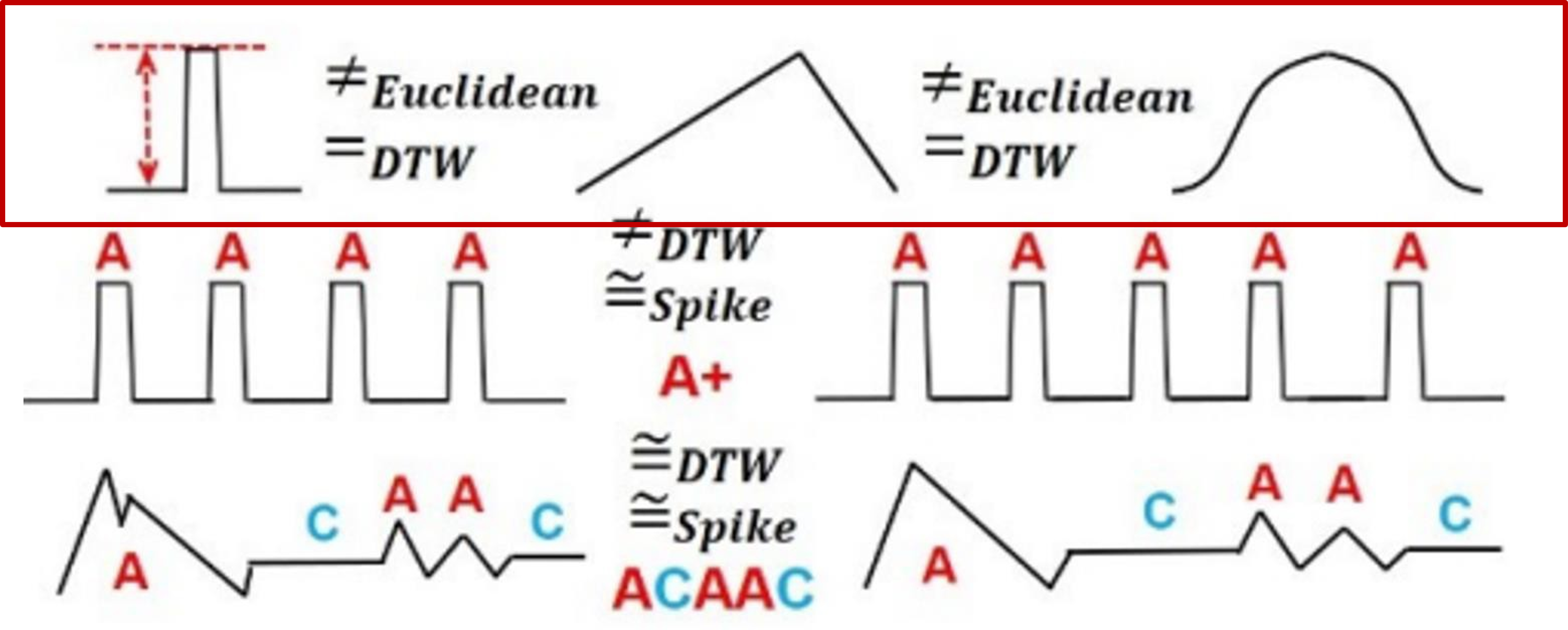
• Limitations of similarity measure for time series
  • 유클리디안, DTW, spike 중에 spike 를사용해야 하는 이유
    • 많은 연구에서 DTW가대부분의 도메인에서 우수한 것을 입증
    • DTW로는 같은 패턴으로 인식 가능, 유클리디안으로는 다른 패턴으로 인식

 

 

 

 

• Limitations of similarity measure for time series
  • 유클리디안, DTW, spike 중에 spike 를사용해야 하는 이유
    • 갯수가 다른 경우, spike는 같게 인식(A+)

 

 

 

• 유사 시계열 차원 감소 기술
  • DWT (Discrete Wavelet Transform)
    • 이산 웨이블릿 변환
    • 시계열 데이터를 다양한 주파수에서 관찰하여 중요한 특징을 추출
    • 고주파 구간은 세밀한 변화를, 저주파 구간은 데이터의 전반적인 추세 나타냄
  • APCA (Adaptive Piecewise Constant Approximation)
    • 데이터를 여러 개의 구간으로 나누고, 각구간을 평균값이나 중간값 등으로 대표하여 데이터의 크기를 줄이는 기법
  • SAX (Symbolic Aggregate approximation)
    • 시계열 데이터를 간결한 기호로 변환하는 방법
    • 원본 데이터를 비교적 작은 수의 심볼로 압축하고, 이심볼들을 사용하여 패턴을 분석하거나 분류하는 데 사용
    • 본논문과 가장 유사한 방법
      • (다른점) SAX는유클리디안 거리를 사용 
      • (다른점) 추출된 패턴에 locked in
        • 추출된 패턴보다 작은 길이의 경우 패턴 찾기 불가
        • (본연구) 다양한 길이의 모티프를 적응적으로 감지할 수있음

 

 

Spikelet

• 시계열 ti: T= t1, t2, ., tn
• 부분 시계열 (서브시퀀스)
  • 수열 T[l:r]는 위치 l에서 시작하여 위치 r까지 T에있는 값들의 연속적인 부분집합
• leg:
  • T[l:r]이 계속 증가하거나, 계속 감소하거나 하는 경우 이를 leg 라고 부름
  • Backward, forward
  • Maximal backward leg: 왼쪽 최대 길이의 leg

 

 

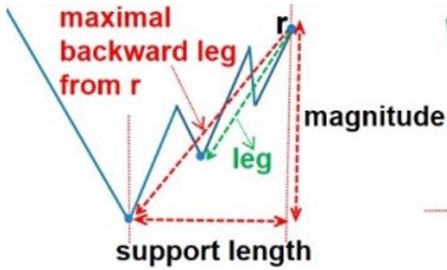
• Maximal leg 두개로 구성된 서브시퀀스 (아래 그림과 같이)
• Positive Spike: Concave 볼록
• Negative Spike: Convex 오목

 

 

 

 

 

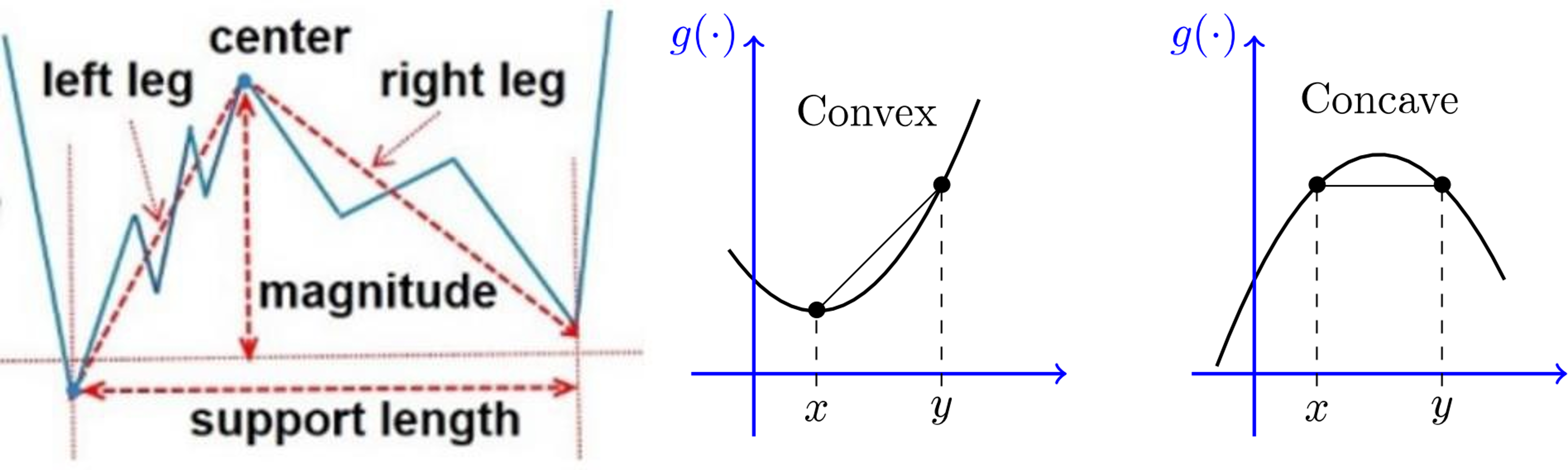
Spikelet Decompositon, operations

• Spike 분해
  • 아래 예시와 같이 연속적으로 추출 가능
  • 인덱스별로 탐색을 하면서 spike를 추출

 

 

 

 

 

 

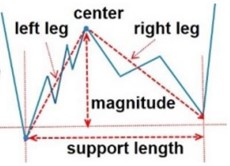
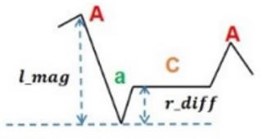
1. positive spike, negative spike로 분해

• 검정: positive spike / 빨강: negative spike

2. magnitude function 으로 표현

3. symbol mapping (기호 매핑)

• Positive, 0, negative : 각각 "A", "a", "C"로 매핑

 

 

 

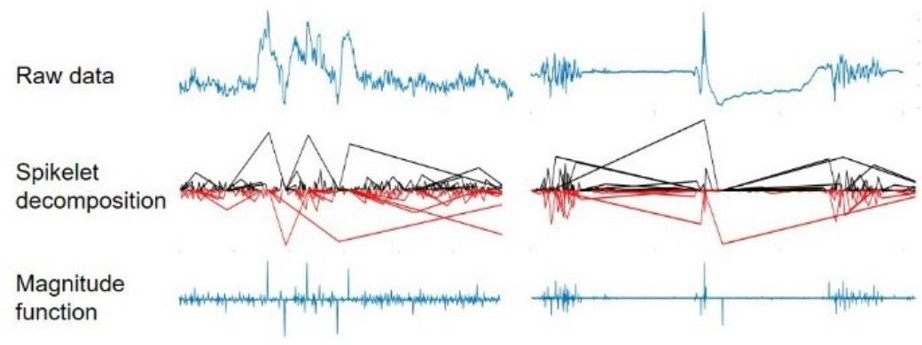
• Spike 분해 과정
  • 1.Global Spike Reduction
  • 2.Constant Segment Extraction
  • 3.Local Spike Reduction

 

 

 

1. Global Spike Reduction

• 파라미터 MagThr 설정
• 본연구 주장: three standard deviation setting 를사용하면 된다
• three standard deviation setting: 데이터 셋의 평균으로부터 세배의 표준편차 범위를 의미

 

 

 

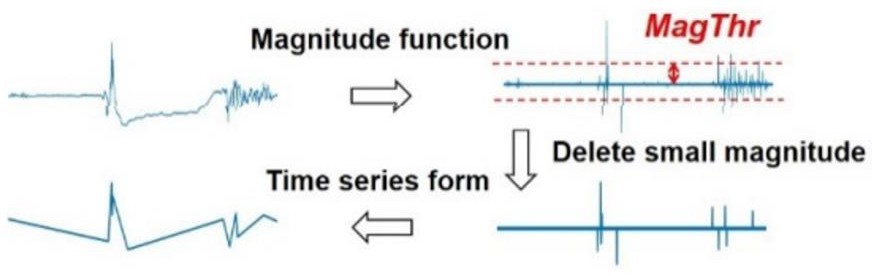
2. Constant Segment Extraction

(1) 고정 구간 찾기

• 일정한 값을 유지하는 구간 찾기
• CLThr 파라미터 설정
• [MagThr] 대역폭 안에 속하는 인덱스의 수가 일정 길이 임계값 [CLThr]보다 크다면, 고정 구간 추출은 이를 고정 구간으로 판단

 

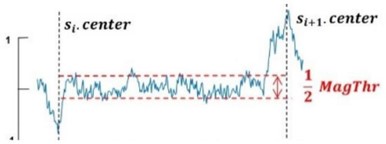
(2) 스파이크 축소

• 고정 구간이 식별되면, 이를 기반으로 스파이크를 줄이거나 수정
• 양면 감소, 일면 감소 (two-sided reduction, one-sided reduction)

• 스파이크가 양쪽에 일정한 세그먼트를 가지고 있고 중앙값과 각 상수값의 차이가 작으면 이 스파이크를 제거
• 스파이크가 한쪽에 일정한 세그먼트를 가지고 있고 중앙값과 상수값의 차이가 반대쪽 다리의 크기에 비해 상대적으로 작으면 이 스파이크를 제거

 

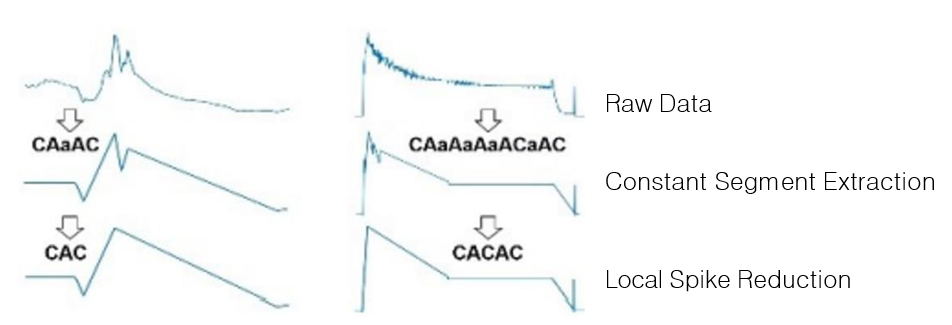
3. Local Spike Reduction

• 작은 스파이크를 식별하여 제거
• 시계열 데이터에서 중요한 패턴이나 구조를 더명확하게 드러내는 데기여
• Constant Segment Extraction
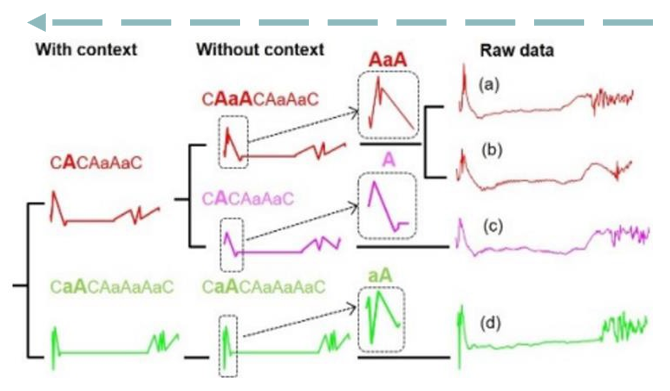
  • 맥락 없는 근사치 approximation without-context
• Local Spike Reduction
  • 맥락 있는 근사치 approximation with-context

 

 

 

Evaluation

• 데이터셋 4개
• 예시
  • Without context -> a, b, c 다른 케이스로 판단
  • With context -> 같은 케이스로 판단
• 결론: With context 적합
• 속도 좋다