Boosting Multimodal Reasoning with MCTS-Automated Structured Thinking 논문 리뷰

Boosting Multimodal Reasoning with MCTS-Automated Structured Thinking

날짜: 2025년 3월 27일

• https://arxiv.org/pdf/2502.02339
• 학습 안하고 MCTS

 

 

Abstract

• 다중 모달 대형 언어 모델(MLLMs)
  • 복잡한 시각적 추론에서 여전히 한계
  • 성능과 효율성의 균형을 맞추는 데 어려움
  • 방대한 데이터와 탐색 공간에 대한 의존도가 높아 비효율적인 암묵적 통찰력 추출과 데이터 활용을 초래
• AStar를 제안
  • 몬테 카를로 트리 탐색(MCTS)을 통한 다중 모달 추론
  • 자동화된 구조적 사로 패러다임
  • → 내부 추론 능력과 외부 추론 가이드를 원활하게 통합한 통합 추론 프레임워크를 설계
  • → 최소한의 트리 반복으로 효율적인 추론

 

 

1. Introduction

• 시스템 2 느린 사고 추론 시스템의 발전
  • 두 가지 주요 접근 방식이 등장: explicit search, teacher supervision-guided training
  • explicit search: 전문화된 보상 모델과 함께 명시적 탐색 구조(예: 몬테 카를로 트리 탐색, MCTS)를 사용하여 해결 경로의 탐색을 안내
  • teacher supervision-guided training: 구조적 추론 패턴을 증류 중점, 긴 형식의 사고 과정 (CoT), GPT-4o와 같은 폐쇄형 모델의 감독
• 현재의 추론 패러다임의 세 가지 주요 한계
  • 탐색 기반 방법(Dong et al., 2024a): 광범위한 솔루션 공간 반복으로 인해 계산 비효율성
  • 교사 지도 교육 방법:
    • 일반적으로 암묵적 추론 패턴을 추출하기 위해 상당한 훈련 데이터 (≥100K)와 계산 자원을 필요
    • 효율성이 낮고 데이터 활용이 저조
    • 데이터 합성을 위해 GPT-4o와 같은 독점 모델에 크게 의존
  • 정적이고 미리 정의된 추론 과정, 유연성을 제한하여 MLLM의 추론 잠재력이 충분히 탐색 X
• AStar를 제안
  • MCTS를 통한 다중 모드 추론을 위한 자동화된 구조적 사고 패러다임
  • 제한된 데이터(500 샘플)를 사용
  • MCTS 기반의 계층 구조에서 고수준의 인지 추론 패턴을 자동으로 도출하기 위한 새로운 메커니즘을 도입 (두 번째 한계 해결)
  • 내부 및 외부의 유리한 속성을 원활하게 통합한 통합 추론 프레임워크를 설계, 최소한의 트리 반복으로 효율적으로 적응할 수 있는 추론 가능하게 함 (첫 번째, 세 번째 한계 해결)
• 세 가지 단계로 구성
  • (1) 시각적 추론 작업 정의, (2) MCTS 기반 사고 카드 구축, (3) 적응형 추론 및 검증
  • (1) 시각적 추론 작업 정의:
    • 사고 구조 패턴의 기본 블록으로 여섯 가지 원자적 추론 작업을 정의
    • 추론 과정에서 참조 통찰로 사용되는 "사고 카드"라고 함
    • 문제 분해와 추론 단계 반영 등 인간과 유사한 인지 행동을 시뮬레이션
  • (2) MCTS 기반 사고 카드 구축
    • 작은 시드 데이터셋(500 샘플)을 사용하여 MCTS를 적용
    • 여러 사고 카드를 구축하기 위한 참조 추론 패턴을 도출
  • (3) 적응형 추론 및 검증
    • 목표 문제의 인지 복잡성과 가장 잘 일치하는 다섯 가지 최적 사고 카드를 선택
• 주요 기여
  • 자동화된 추론 패러다임: 최적의 추론 패턴을 생성 및 선택하기 위한 MCTS 기반의 자동화된 접근 방식을 제안
  • 효율적인 작업 체인 가이드 추론: 시각적 추론 과정의 각 단계에 대한 명시적 가이드를 제공하여 구조적 사고 능력을 향상
  • 뛰어난 성능
  • 향상된 효율성:
    • 최근 트리 기반 방법과 유사한 성능을 달성하면서 추론 오버헤드를 6.4배 줄임
    • 훈련 기반 방법과 일치시키면서 520배 적은 이전 데이터를 요구

 

 

2. Related Work

• Multimodal Reasoning
  • MLLM의 최근 발전은 시각적 이해: 수학, 과학 등 다양한 분야 강력한 성능
  • 복잡한 다중 양식 추론은 시각적 인식과 고급 인지에 대한 요구로 인해 여전히 도전적
  • 최근 연구: OpenAi 영감
    • 구조화된 추론을 시도하여 MLLM의 CoT 능력을 향상
    • → 이들의 경직된 구조: 다양한 작업에서의 유연성을 제한, 적응형 추론의 중요성을 간과
  • 본 연구: 작업별 추론 경로 생성을 가능하게 하는 계층적 트리 구조를 도입하여 이러한 문제를 해결
• Tree-based Search
  • 트리 구조는 언어 모델에서 상당한 잠재력을 입증
  • 최근 연구: MLLM에 접목
    • AR-MCTS: MCTS와 능동적 검색을 통합하여 다중 양식 추론을 향상, 광범위한 반복 요구와 계산 오버헤드로 인해 실제 응용에 제한
    • Mulberry: GPT-4o와 같은 강력한 모델에서 260K의 긴 체인 추론 데이터를 정제하기 위해 트리 구조를 활용, 상당한 계산 자원과 고용량 교사 모델이 필요
    • → 성능과 효율성 사이의 최적 균형 달성에 어려
  • 본 연구: MCTS에 고급 추론 추상화를 통합하여 더 높은 효율성으로 경쟁력 있는 성능을 달성

 

 

3. Methodology

• Overview of AStar
  • 시각적 추론 행동 정의: 체인 구조의 사고 카드 생성을 위한 여섯 가지 인간과 유사한 추론 행동을 구축 블록으로 설정
  • MCTS 기반 사고 카드 구성: MCTS를 활용하여 사고 카드를 체계적으로 구성, 이는 추론 시 참조 통찰로 작용
  • 적응형 추론 및 검증: 문제의 복잡도에 따라 최적의 추론 패턴을 동적으로 선택하고 실행, 솔루션을 검증

 

 

3.1 Visual Reasoning Action Definition

• 기존 연구: 두 가지 인지 시스템을 구분 → 시스템1, 시스템2
  • 시스템1: 빠르고 직관적이며 오류가 발생하기 쉬운 사고
  • 시스템2: 느리고 심사숙고하는 사고로 더 우수한 성과
  • 시스템2 주목 받고 있음 (OpenAI, 인간 인지 과정 모방)
• 본 연구: 여섯 가지 비전-언어 추론 작업을 소개
  • 비주얼 파싱 (VP, a1), 시스템 분석 (SA, a2), 일단계 사고 (OST, a3), 사고의 연쇄 (CoT, a4), 분할 정복 (DC, a5), 자기 반성 (SR, a6)

 

 

3.2 MCTS-Powered Thought Card Construction

• 작업 정의에 따라, "사고 카드"를 구조화된 추론 템플릿으로 소개
  • 소규모 시드 데이터 세트를 사용
  • 추론 경로를 유도(1단계)
  • 고수준 사고 카드로 증류(2단계)
  • 카드는 추론 중에 구조화된 지침을 제공하여 효율적인 문제 적응형 추론을 위한 사전 통찰로 사용
• Phase 1: Acquire reasoning paths for seed data (MCTS(Monte Carlo Tree Search))
  • 루트 노드: 각 다중 모드 추론 문제 x (입력 질문과 이미지로 구성), 트리 검색 문제로 정의
  • 후속 노드: 정책 모델인 MLLM πθ가 생성한 추론 단계(행동과 결과)
    • 상태 St-1은 경로 x, s1, ..., st-1로 정의, S0 = x로 시작
    • 다음 단계는 πθ (St-1)에서 샘플링
    • 트리 확장을 유도하기 위해 각 노드의 Q(s) 값을 보상으로 정의,
  • 네 가지 주요 작업
    • 선택(Selection): 루트 노드에서 시작하여, UCT(Upper Confidence Bounds applied to Trees) 알고리즘을 사용하여 자식 노드를 선택, 탐색과 활용을 균형 있게 수행
    • 확장(Expansion): 선택된 노드에서 πθ로부터 여러 액션을 샘플링, 자식 노드를 확장하고 트리에 추가
    • 시뮬레이션(Simulation): 선택된 노드에서 시작해 노드를 반복적으로 확장하여 종결 상태(최대 깊이 또는 답변 노드)에 도달할 때까지 진행
    • 역전파(Backpropagation): 시뮬레이션이 끝나면, 시뮬레이션 경로를 따라 노드 정보를 업데이트하고, 방문 횟수와 Q(s) 값을 부모 노드로 전파
• Phase 2: Distill paths into thought cards
  • MCTS 실행 이후, 각 시드 데이터 세트 질문에 대한 트리 구조를 얻어 다수의 유효한 추론 경로로 구성된 경로 집합 P를 생성
  • 경로 집합(P)을 구성
  • 계산의 가치(Value of Computation, VOC) 개념에서 영감
    • 계산 이점과 비용 사이의 균형을 최적화하는 VOC-inspired 선택 지표를 사용하여 최적의 추론 경로를 선택
    • 경로의 최종 보상(즉, 리프 노드의 Q 값), 추론 비용(경로에 포함된 행동의 수) C(px) 를 계산
  • 질문-경로 쌍: PCC(문제 조건 복잡도, Problem Condition Complexity)라는 인지적 복잡도 지표를 사용해, 추상화된 사고 카드 C로 증류

 

 

3.3 Adaptive Reasoning and Verification

• 추론 시, 멀티모달 테스트 쿼리 $x_t$
• PCC 계산, 사전 구성된 사고 카드 C에 대해 최근접 이웃 매칭 수행
• 복잡성 수준과 가장 잘 일치하는 가장 관련성 높은 다섯 개 카드 선정

 

 

4. Experiments

4.1 Experimental Setup

• 데이터셋: 세 가지 추론 작업과 여섯 개 데이터셋에서 광범위한 실험
  • (1) 일반 시각 질문 답변
  • (2) 수학적 추론
  • (3) 상식 및 과학적 추론
• 모델: LLM과 MLLM 모두에서 그 효과를 평가
  • Qwen2.5-7B, Qwen2-VL-2B, Qwen2-VL-7B
  • 사전 훈련된 LLM 및 MLLM을 수정 없이 추론 백본으로 원활하게 활용할 수 있음을 검증하는 것을 목표
• 베이스라인: 네 가지 강력한 기준선 범주와 비교 평가
  • (1) 강력한 오픈소스 일반 MLLM, Qwen2-VL 및 InternVL2 시리즈
  • (2) 수학적 추론에 최적화된 오픈소스 MLLM
  • (3) 고급 폐쇄형 MLLM, GPT-4V 및 GPT-4o
  • (4) 트리 기반 방법, AR-MCTS, Mulberry

 

 

4.2 Performance Comparison with Baselines

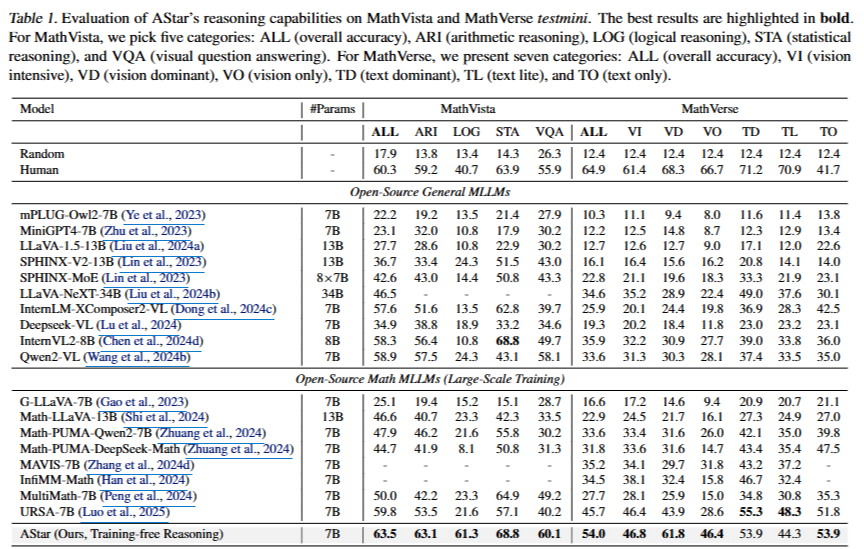
• Results on Diverse Reasoning Benchmarks
  • AStar는 일반 시각 질문 답변 및 수학적 추론 작업에서 강력한 오픈소스와 수학 전문 MLLM 모두를 지속적으로 초과
  • AStar는 여러 추론 능력에서 강력한 성능
  • AStar의 적응형 추론의 장점은 보편적이며 다양한 멀티모달 정보 내용의 정도에 따라 일관된 성능 향상을 유지
  • AStar는 전문적인 추론 작업을 넘어 일반 VQA 벤치마크(MMStar 및 ChartQA)에서도 우수한 성능을 발휘

 

 

 

• Results on More Challenging Datasets
  • AStar는 여러 추론 차원에서 도전적인 MathVision 벤치마크에서 선도적인 모델들과 평가

 

 

 

• Comparison with Leading MLLMs
  • AStar를 선도적인 폐쇄형 및 대형 오픈 소스 모델과 비교
  • AStar 기반 모델은 경쟁력 있는 성능을 제공하며, 대형 모델과 비슷하거나 이를 초과하는 성능

 

 

 

4.3 Data and Computational Efficiency

• 경쟁력 있는 성능을 달성하면서도 데이터 및 계산 효율성을 크게 향상
  • 데이터 효율성 측면: AStar는 0.5K의 샘플만 필요, AR-MCTS(34.5K)에 비해 69배 감소하고 Mulberry(260K)에 비해 520배 감소한 수치
  • 계산 효율성 측면: AStar는 AR-MCTS에 비해 샘플당 평균 이터레이션 수를 6.4배 줄이면서 모든 벤치마크에서 유사하거나 우수한 정확도를 유지

 

 

4.4 Out-of-Distribution Generalization

• 최근 연구: 분포 변화가 MLLM의 신뢰성에 심각한 영향을 미친다는 점을 강조
  • 모델은 분포 내(ID) 작업에서 뛰어난 성능을 발휘하지만, 분포 밖(OOD) 시나리오에서는 성능이 종종 저하
  • 문제는 충분한 고품질 훈련 데이터를 확보하는 것이 어렵다는 점에서 더욱 복잡
• 본 모델: 추론이 수학 분야 기준
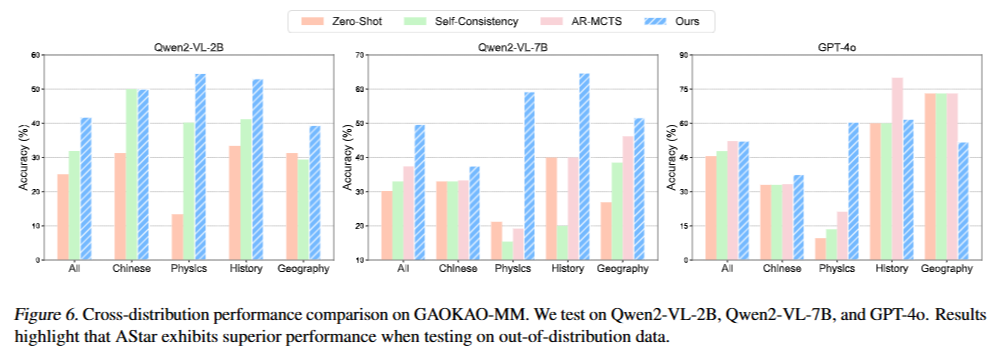
  • GAOKAO-MM (Zong & Qiu, 2024)에서 추가적인 테스트를 수행
  • GAOKAO-MM: 역사적, 지리적, 과학적 추론 작업을 포함하는 중국의 인간 수준 다중 모드 추론 벤치마크
  • 자연스럽게 OOD 평가 설정을 구성 가능
• 결과) AStar 프레임워크로 향상될 때 기준 방법에 비해 상당한 개선
  • AStar의 다양한 언어, 작업 분포 및 추론 도메인에서의 강력한 일반화를 검증
  • ID 및 OOD 추론 작업을 위한 강력하고 다재다능한 접근 방식

 

 

4.5 Ablation Study and Analysis

• Ablation Study 세 가지 주요 발견
  • 어떤 구성 요소를 제거하더라도 성능 저하가 발생하여 모든 구성 요소 설계의 필수성 검증
    • 카드 구성 모듈을 제외하면 가장 큰 성능 저하가 발생
  • 카드 일치 card matching의 정밀도도 성능에 영향
    • MathVerse와 같은 복잡한 작업에서는 저하가 MathVista보다 더 뚜렷
    • PCC 기반의 최근접 이웃 일치를 사용, 향후 더 발전된 전략 탐구
  • 검증 모듈은 성능을 개선. 자기 일관성 (SC) 또는 무작위 선택 (RS)과 같은 더 간단한 대안은 상대적으로 경미한 저하(2.0% 및 1.4%)
• Inference Time Scaling
  • 추론 중에 선택된 생각 카드의 수를 점진적으로 증가, 테스트 시간 확장 법칙을 따르는지 조사
  • AStar 프레임워크에서 지속적인 성능 향상이 발생

 

 

• Visualization of Sampling Space
  • AStar 기반 추론 프레임워크가 다양한 수의 사고 카드를 사용할 때 생성하는 솔루션의 다양성을 분석하기 위해 시각화 연구 진행
    • MathVision에서 250개의 문제를 샘플링, 각 문제에 대해 2개의 후보 솔루션을 생성, 총 500개의 샘플을 생성
    • 의미적 임베딩을 위한 BGE-M3 (Chen et al., 2024a)를 사용, 차원 축소(PCA)와 클러스터링 기법(DBSCAN, Ester et al., 1996)을 적용
  • 그림 8과 9는 MathVista와 MathVision에서 사고 카드 수(k = 2와 k = 5)에 따른 시각화 결과
    • 사고 카드가 적을 때(k = 2), 모델은 동일한 문제 집합에 대해 더 적은 중심점을 가진 클러스터를 생성 (=제한된 잠재력을 가진 제약된 샘플링 공간)
    • MathVista에서 MathVision보다 더 낮은 클러스터 수가 관찰.
      • MathVista가 비교적 간단한 문제 포함
      • → 강력한 추론 경로 수렴
      • MathVision 데이터셋에서는 더 큰 경로 분기가 관찰

 

 

 

5. Conclusion

• AStar
  • MCTS(몬테카를로 트리 탐색)의 계층적 구조를 활용
  • 시각 추론 작업에서 성능과 효율성 문제를 효과적으로 해결